
题目列表(包括答案和解析)
1.直线y=-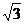 x+1的倾斜角为 .
x+1的倾斜角为 .
20.解:已知函数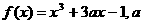 为实常数.
为实常数.
(1)a在什么范围内时, 只有一个公共点?
只有一个公共点?
(2)若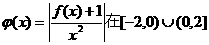 上有最小值2,求a的值.
上有最小值2,求a的值.
[解析](1) .
.
①当 时,
时, ,所以
,所以 在R上单调增,此时
在R上单调增,此时 只有一个公共点;
只有一个公共点;
②当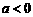 时,
时, .由
.由 ,得
,得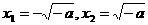 .
.
在 上列表:
上列表:
 |
 |
 |
 |
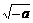 |
 |
 |
+ |
0 |
─ |
0 |
+ |
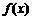 |
↗ |
极大值 |
↘ |
极小值 |
↗ |
因为 只有一个公共点,所以
只有一个公共点,所以 或
或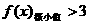 .
.
所以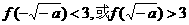 ,得
,得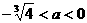 .
.
综上, ,
, 只有一个公共点.
只有一个公共点.
(2) .
.
由 ,可知
,可知 为偶函数,则原题即为
为偶函数,则原题即为 在
在 上有最小值2.
上有最小值2.
设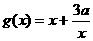 (
( ),则
),则 .
.
① 时,
时, ,所以
,所以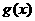 在
在 上单调增,所以
上单调增,所以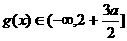 .
.
因为 在
在 上有最小值2,所以
上有最小值2,所以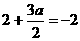 ,所以
,所以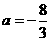 .
.
② 时,
时,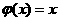 ,无最小值,不合题意.
,无最小值,不合题意.
③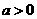 时,
时, ,
, .
.
(I) ,即
,即 时,
时,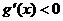 ,所以
,所以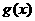 在
在 上单调减,所以
上单调减,所以 ,此时
,此时 在
在 上的最小值为
上的最小值为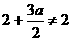 ,不合题.
,不合题.
(II)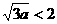 ,即
,即 时,由
时,由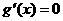 ,得
,得 .
.
在 上列表:
上列表:
 |
 |
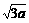 |
 |
2 |
 |
─ |
0 |
+ |
|
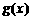 |
↘ |
极小值 |
↗ |
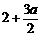 |
∴ ,即
,即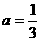 .综上,
.综上, 的值为
的值为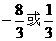 .
.
18.证法一:∵b>a>e,∴要证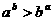 ,只要证blna>alnb,设f(b)=blna-alnb(b>e),则
,只要证blna>alnb,设f(b)=blna-alnb(b>e),则
f′(b)=lna-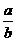 .∵b>a>e,∴lna>1,且
.∵b>a>e,∴lna>1,且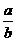 <1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴
<1,∴f′(b)>0.∴函数f(b)=blna-alnb在(e,+∞)上是增函数,∴f(b)>f(a)=alna-alna=0,即blna-alnb>0,∴blna>alnb,∴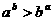 .
.
证法二:要证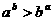 ,只要证blna>alnb(e<a<b
,只要证blna>alnb(e<a<b ,即证
,即证 ,设f(x)=
,设f(x)= (x>e),则f′(x)=
(x>e),则f′(x)= <0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
<0,∴函数f(x)在(e,+∞)上是减函数,又∵e<a<b,
∴f(a)>f(b),即 ,∴
,∴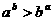 .
.
19解:物体的速度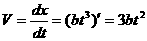 .媒质阻力
.媒质阻力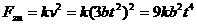 ,其中k为比例常数,k>0.
,其中k为比例常数,k>0.
当x=0时,t=0;当x=a时,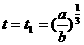 ,又ds=vdt,故阻力所作的功为
,又ds=vdt,故阻力所作的功为
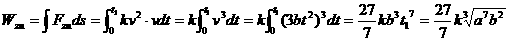
17. 解:(Ⅰ)
令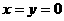 ,得
,得
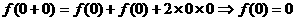 ……
……
证明:(Ⅱ) ,
,
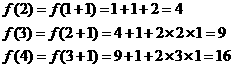
猜想 ,下用数学归纳法证明之.
,下用数学归纳法证明之.
(1)当n=1时,f(1)=1,猜想成立;
(2)假设当n=k时,猜想成立,即 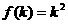 ,
,
则当n=k+1时, f(k+1)=f(k)+f(1)+2k×1=k2+2k+1=(k+1)2
即当n=k+1时猜想成立。
由(1)、(2)可知,对于一切n∈N*猜想均成立。
15解:由已知得 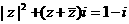
设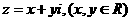 ,代入上式得
,代入上式得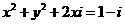
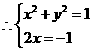 ,解得
,解得
故复数 为
为 分
分
16、 解:由
解:由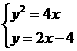 得交点坐标为
得交点坐标为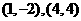 ,如图
,如图
(或答横坐标)
方法一:阴影部分的面积
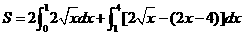
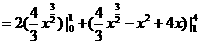
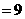
方法二:阴影部分的面积 
 = 9
= 9
方法三:直线与 轴交点为(2,0)所以阴影部分的面积
轴交点为(2,0)所以阴影部分的面积

 = 9
= 9
12.2,3;13.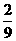 ,;14.
,;14.
9. ;10.41;
;10.41; ;11.
;11.
20. (14分)
|
高二数 学(理科)答案及评分标准
18. (14分)
|
19(14分)
|
15.(12分)
_16. 16。(12分)
.
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com