
题目列表(包括答案和解析)
21.(本题满分14分)本题共有2个小题,第1小题
满分5分,第2小题满分7分.
 如图,某隧道设计为双向四车道,车道总宽22米,要
如图,某隧道设计为双向四车道,车道总宽22米,要
求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.
(1)若最大拱高 为6米,则隧道设计的拱
为6米,则隧道设计的拱
宽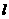 是多少?
是多少?
(2)若最大拱高 不小于6米,则应如何设
不小于6米,则应如何设
计拱高 和拱宽
和拱宽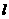 ,才能使半个椭圆形隧道的
,才能使半个椭圆形隧道的
土方工程量最最小?
(半个椭圆的面积公式为 ,柱体体积为:底面积乘以高.)
,柱体体积为:底面积乘以高.)
20. (本小题满分12分)如图,
(本小题满分12分)如图, 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线内一定点,
为抛物线内一定点,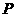 为抛物线上一动点,且
为抛物线上一动点,且 的最小值为8.
的最小值为8. 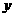
(1)求该抛物线方程; P
(2)如果过 的直线
的直线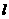 交抛物线于
交抛物线于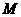 、
、 两点,
A
两点,
A
且 ,求直线
,求直线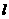 倾斜角的取值范围.
O F
倾斜角的取值范围.
O F

19.(本小题满分12分)已知点 、
、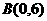 ,
, 为坐标原点.
为坐标原点.
(1)若点 在线段
在线段 上,且
上,且 ,求
,求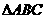 的面积;
的面积;
(2)若原点 关于直线
关于直线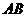 的对称点为
的对称点为 ,延长
,延长 到
到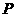 ,且
,且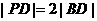 .已知直线
.已知直线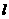 :
: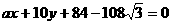 经过点
经过点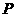 ,求直线
,求直线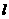 的倾斜角.
的倾斜角.
18.(本小题满分12分)已知圆 ,
,
(1)若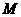 为圆上任一点,
为圆上任一点, ,求
,求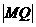 的最大值和最小值;
的最大值和最小值;
(2)求 的最大值和最小值;
的最大值和最小值;
(3)求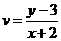 的最大值.
的最大值.
17.(本小题满分12分)已知椭圆的焦点为 和
和 ,直线
,直线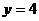 是椭圆的一条准线.
是椭圆的一条准线.
(1)求椭圆的方程;
(2)又设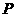 在此椭圆上,且
在此椭圆上,且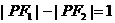 ,求
,求 的值.
的值.
16.给出问题:F1、F2是双曲线 =1的焦点,点P在双曲线上.若点P到焦点F1的距
=1的焦点,点P在双曲线上.若点P到焦点F1的距
离等于9,求点P到焦点F2的距离.某学生的解答如下:
双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内,若不正确,将正确
的结果填在下面空格内.
_____________________________________________________________________________.
15.若直线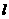 沿
沿 轴负方向平移3个单位,再沿
轴负方向平移3个单位,再沿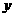 轴正方向平移一个单位后,又回到原来的位置,那么直线
轴正方向平移一个单位后,又回到原来的位置,那么直线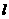 的斜率为
的斜率为 .
.
14. 如图,F1,F2分别为椭圆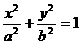 的左、右焦点,
的左、右焦点,
点P在椭圆上,△POF2是面积为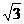 的正三角形,则
的正三角形,则
 的值是
.
的值是
.
13.抛物线的顶点在原点,对称轴是坐标轴,且焦点在直线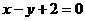 上,则此抛物线方程为__________________.
上,则此抛物线方程为__________________.
12.已知双曲线中心在原点且一个焦点为 直线
直线 与其相交于M、N两点,
与其相交于M、N两点,
MN中点的横坐标为 则此双曲线的方程是( )
则此双曲线的方程是( )
A.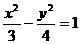 B.
B.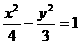 C.
C.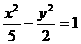 D.
D.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com