
题目列表(包括答案和解析)
4.已知m,n∈R,则“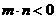 ”是“方程
”是“方程 表示双曲线”的(
)
表示双曲线”的(
)
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
3.一个容量为20的样本数据,分组后,组别与频数如下:
|
组别 |
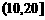 |
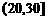 |
 |
 |
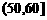 |
 |
||||||||||||||||||||||||
|
频数 |
2 |
3 |
4 |
5 |
4 |
|
则样本在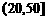 上的频率为(
)
上的频率为(
)
A.12% B.40% C.60% D.70%
高二数学(文科)试题 第1页(共4页)
2.已知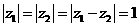 ,则
,则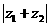 等于( )
等于( )
A. B.
B. C.
C. .
D.
.
D.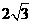
1.
复数 的共轭复数是( )
的共轭复数是( )
A. B.
B.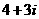 C.
C.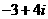 D.
D.
22.
 如图,过点P(1,0)作曲线C:
如图,过点P(1,0)作曲线C:  的切线,切点为
的切线,切点为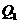 ,设
,设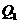 点在x轴上的投影是点
点在x轴上的投影是点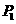 ;又过点
;又过点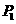 作曲线C的切线,切点为
作曲线C的切线,切点为 ,设
,设 在x轴上的投影是
在x轴上的投影是 ;…;依此下去,得到一系列点
;…;依此下去,得到一系列点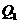 ,
, ,…,
,…,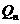 ,…,设点
,…,设点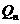 的横坐标为
的横坐标为 .
.
(Ⅰ)试求数列{ }的通项公式
}的通项公式 ;(用
;(用 的代数式表示)
的代数式表示)
(Ⅱ)求证:
(Ⅲ)求证: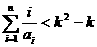 (注:
(注: ).
).
解: (Ⅰ) 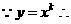
 ,若切点是
,若切点是 ,则
,则
切线方程为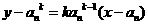 .
1分
.
1分
当n=1时,切线过点(1,0),即 ,得
,得
当n>1时,切线过点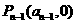 ,即
,即 ,解得
,解得 .
.
 数列
数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
故所求通项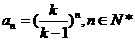 .
4分
.
4分
(Ⅱ) 由(1)知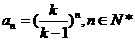

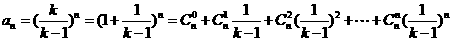
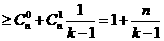 9分
9分
(Ⅲ)设 ,则
,则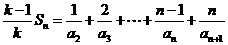 ,
,
两式相减得 ,
,

 . 故
. 故 .
14分
.
14分
21、(本小题满分12分)已知函数 ,在
,在 处取得极值为2。
处取得极值为2。
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)若函数 在区间(m,2m+1)上为增函数,求实数m的取值范围;
在区间(m,2m+1)上为增函数,求实数m的取值范围;
(Ⅲ)若P(x0,y0)为 图象上的任意一点,直线l与
图象上的任意一点,直线l与 的图象相切于点P,求直线l的斜率的取值范围.
的图象相切于点P,求直线l的斜率的取值范围.
解:(Ⅰ)已知函数 ,
,
 …………1分
…………1分
又函数 在
在 处取得极值2,
处取得极值2, …………2分
…………2分
即
 ……………………4分
……………………4分
(Ⅱ) 由
由 ,得
,得 ,
,
即
所以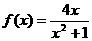 的单调增区间为(-1,1) …………6分
的单调增区间为(-1,1) …………6分
因函数 在(m,2m+1)上单调递增,
在(m,2m+1)上单调递增,
则有 , …………7分
, …………7分
解得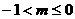 即
即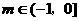 时,函数
时,函数 在(m,2m+1)上为增函数 …………8分
在(m,2m+1)上为增函数 …………8分
(Ⅲ)
直线l的斜率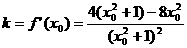 …………9分
…………9分
即
 令
令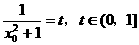 , …………10分
, …………10分
则
 即直线l的斜率k的取值范围是
即直线l的斜率k的取值范围是 …………12分
…………12分
20.(本小题满分12分)
已知函数 ,在x=1处连续.
,在x=1处连续.
(I)求a的值;
(II)求函数 的单调减区间;
的单调减区间;
(III)若不等式 恒成立,求c的取值范围.
恒成立,求c的取值范围.
(I)解:由 处连续,
处连续,
可得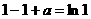 ,故
,故 …………3分
…………3分
(II)解:由(I)得

所以函数 …………7分
…………7分
(III)解:设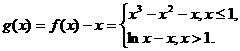
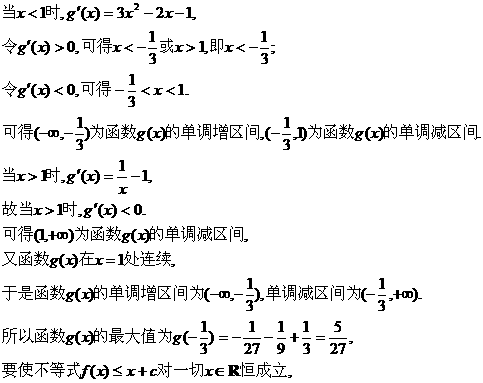

故c的取值范围为 …………12分
…………12分
19.(本小题满分12分)如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,
SD⊥AB,且AB=2AD,SD=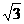 AD,
AD,
(Ⅰ)求证:平面SDB⊥平面ABCD;
(Ⅱ)求二面角A-SB-D的大小.
解:(1)∵SD⊥AD,SD⊥AB,AD∩AB=A
∴SD⊥平面ABCD,
又∵SD 平面SBD, ∴平面SDB⊥平面ABCD。 …………5分
平面SBD, ∴平面SDB⊥平面ABCD。 …………5分
(2)[解法一]:由(1)知平面SDB⊥平面ABCD,
BD为平面SDB与平面ABCD的交线,过点A作AE⊥DB于E,则AE⊥平面SDB,
又过点A作AF⊥SB于F,连结EF。
由三垂线定理的逆定理得 EF⊥SB,
∴∠AFE为二面角A-SB-D的平面角。 …………8分
在矩形ABCD中,设AD=a,
则 ,
,
 在Rt△SBC中,
在Rt△SBC中,
而在Rt△SAD中,SA=2a,又AB=2a,
∴SB2=SA2+AB2, …………10分
即△SAB为等腰直角三角形,且∠SAB为直角,
∴
∴
故二面角A-SB-D的大小为
 …………12分
…………12分
[解法二]:由题可知DS、DA、DC两两互相垂直。
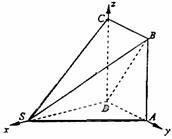 如图建立空间直角坐标系D-xyz
如图建立空间直角坐标系D-xyz
设AD=a,
则S(

∵ --------------------7分
--------------------7分
设面SBD的一个法向量为n=(x,y,-1)
则
解得 n=(0,2,-1)--------------------9分
又∵

设面SAB的一个法向量为m=(1,y,z),
则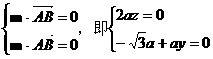
解出
m=(1,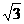 ,0), --------------------11分
,0), --------------------11分

故所求的二面角为arccos --------------------12分
--------------------12分
|
18.(本小题满分12分)省教研室准备举行一次高中数学新课程研讨会,共邀请50名一线教师参加,使用不同版本教材的教师人数如下表所示:
|
版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
|
人数 |
20 |
15 |
5 |
10 |
(1)从这50名教师中随机选出2名,求2人所使用版本相同的概率;
(2)若随机选出2名使用人教版的教师发言,设使用人教A版的教师人数为 ,求随机变量
,求随机变量 的变分布列和数学期望。
的变分布列和数学期望。
解:(1)从50名教师随机选出2名的方法数为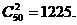
选出2人使用版本相同的方法数为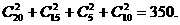
故2人使用版本相同的概率为:
 ………5分
………5分
(2)∵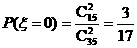 ,
, 

 |
0 |
1 |
2 |
|
P |
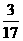 |
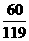 |
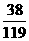 |
∴ 的分布列为
的分布列为
…………10分
∴ …………12分
…………12分
( 可以不扣分)
可以不扣分)
17.(本小题满分12分)
某车间在三天内,每天生产10件某产品,其中第一天,第二天分别生产出了1件、2件次品,而质检部每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(Ⅰ)求第一天通过检查的概率;
(Ⅱ)求前两天全部通过检查的概率;
(Ⅲ)若厂内对车间生产的产品采用记分制:两天全不通过检查得0分,通过1天、2天分别得1分、2分,求该车间在这两天内得分 的数学期望.
的数学期望.
解:(I) 随意抽取4件产品检查是随机事件,而第一天有9件正品
随意抽取4件产品检查是随机事件,而第一天有9件正品
 第一天通过检查的概率为
第一天通过检查的概率为 ……3分
……3分
(II)同(I),第二天通过检查的概率为
因第一天,第二天是否通过检查相互独立
所以,两天全部通过检查的概率为: ……6分
……6分
(Ⅲ)记得分为 ,则
,则 的值分别为0,1,2
的值分别为0,1,2


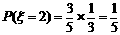
因此, ……12分
……12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com