
题目列表(包括答案和解析)
2.一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
A.至多有一次中靶 B.两次都中靶
C.只有一次中靶 D.两次都不中靶
1.一组数据中的每一个数据都减去80,得到新数据,若求得新数据的平均数是1.2,则原来数据的平均数是( )
A. B.
B. C.
C. D.不能确定
D.不能确定
22、解:(1)

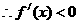
因此函数ƒ( )在区间(0,+
)在区间(0,+ )上是减函数. ............3分
)上是减函数. ............3分
(2)证明:当 >0时,ƒ(
>0时,ƒ( )>
)> 成立,即证当
成立,即证当 >0时,(
>0时,( +1)ln(
+1)ln( +1)+1-2
+1)+1-2 >0成立.
>0成立.
令g( )=(
)=( +1)ln(
+1)ln( +1)+1-2
+1)+1-2 ,则
,则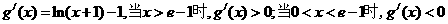 ,
,

 .
.
 .
............8分
.
............8分
(3)由(2)知: ,
,
 ,
,
令 .
.
 ln(1+1·2)+ln(1+2·3)+…+ln[1+n(n+1)]
ln(1+1·2)+ln(1+2·3)+…+ln[1+n(n+1)]
>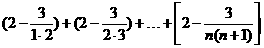
=

= ,
,
 .
............14分
.
............14分
21、解: (1)解法一
设
当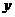 ≥-2时;
≥-2时; ;
;
当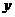 <-2时,
<-2时,
两边平方得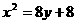 ,因
,因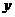 <-2,不合题意,舍去.
<-2,不合题意,舍去.
故点M的轨迹C的方程是: .
............4分
.
............4分
解法二 ∵点M到点F(0,1)的距离比它到直线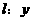 =-2的距离小1.
=-2的距离小1.
∴点M在直线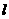 的上方. ∴点M到F(0,1)的距离与它到直线
的上方. ∴点M到F(0,1)的距离与它到直线 =-1的距离相等.
=-1的距离相等.
∴点M的轨迹C是以F为焦点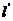 为准线的抛物线,所以曲线C的方程为
为准线的抛物线,所以曲线C的方程为 .
.
(2)当直线m的斜率不存在时,它与曲线C只有一个交点,不合题意,
当直线m与 轴不垂直时,设直线m的方程为
轴不垂直时,设直线m的方程为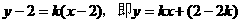 .
.
代入 得,
得,
 ①
①
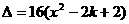 >0对k∈R恒成立.
>0对k∈R恒成立.
∴直线m与曲线C恒有两个不同的交点。
设交点A,B的坐标分别为A( )B(
)B(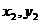 ),则
),则 .
.  .
.
(i)由 ,且λ=1得,P为AB的中点,
,且λ=1得,P为AB的中点,
∴ .把②代入得,
.把②代入得,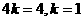 .∴直线m的方程是
.∴直线m的方程是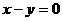 .
.
............6分
(ii) =
=
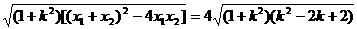 .
.
点O到直线m的距离 .
.
 =
= ·
· =
=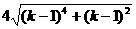
∵ =
=
∴ .
.
(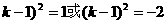 (无实根)
(无实根)
由
1°当k=0时,方程①的解为 .
.
当 =
= ;
;
当 . ...........10分
. ...........10分
2°当k=2时,方程①的解为 ,
,
同理可得,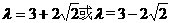 .
............12分
.
............12分
20、解: (1)由题设知
 ƒ(
ƒ( )=
)= 3+2
3+2 2+
2+ ,
,
则 ,
,
令 ,
,
当 变化时,ƒ(
变化时,ƒ( )
) 的变化情况如下表:
的变化情况如下表:
 |
(- ,-1) ,-1) |
-1 |
(-1, ) ) |
 |
( + + ) ) |
 |
+ |
0 |
- |
0 |
+ |
ƒ( ) ) |
↑ |
0 |
↓ |
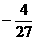 |
↑ |
 ƒ(
ƒ( )的极大值为ƒ(-1)=0,极小值为ƒ(
)的极大值为ƒ(-1)=0,极小值为ƒ( )=
)= .............6分
.............6分
(2) 3+2
3+2 2+
2+ ≥
≥

 .
.
考虑方程 根的情况,
根的情况,
若 >0,则方程
>0,则方程 的根为
的根为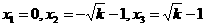 ,
,
①当 >1时,
>1时,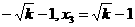 ,
,
 ;
;
② =1时,不等式的解集为
=1时,不等式的解集为 ;
;
③0< <1时,
<1时, ;
;
若 =0时,不等式的解集为
=0时,不等式的解集为 ;
;
若 <0时,不等式的解集为
<0时,不等式的解集为 .............12分
.............12分
19、解:(1) PA=AB=2
PA=AB=2 ,PB=
,PB= ,
, PA2+AB2=PB2,
PA2+AB2=PB2, ∠PAB=90O,即PA⊥AB.同理PA⊥AE.又
∠PAB=90O,即PA⊥AB.同理PA⊥AE.又 AB∩AE=A,
AB∩AE=A, PA⊥平面ABCDE. ............4分
PA⊥平面ABCDE. ............4分
 (2)解法一 如图,
(2)解法一 如图, ∠DEA=90O,
∠DEA=90O,
 AE⊥ED.
AE⊥ED.  PA⊥平面ABCDE,
PA⊥平面ABCDE, PA⊥ED.
PA⊥ED.
又 PA∩AE=A,
PA∩AE=A, ED⊥平面PAE.过A作
ED⊥平面PAE.过A作
AG⊥PE于G, DE⊥AG,
DE⊥AG, AG⊥平面PDE.
AG⊥平面PDE.
过G作GH⊥PD于H,连结AH,由三垂线定理
得AH⊥PD.  ∠AHG为二面角A-PD-E的平面
∠AHG为二面角A-PD-E的平面
角.在直角△PAE中,AG=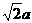 .在直角△PAD中,
.在直角△PAD中,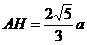 ,
, 在直角△AHG中,sin∠AHG=
在直角△AHG中,sin∠AHG= .
.
 ∠AHG=arcsin
∠AHG=arcsin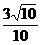 ,
, 二面角A-PD-E的大小为arcsin
二面角A-PD-E的大小为arcsin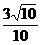 . ............12分
. ............12分
 解法二 建立如图所示的空间直角坐标系,则B(2
解法二 建立如图所示的空间直角坐标系,则B(2 ,0,0),E(0,2
,0,0),E(0,2 ,0),P(0,0,2
,0),P(0,0,2 ),D(
),D( ,2
,2 ,0),
,0),
C(2 ,
, ,0),过A作AN⊥PD于N.
,0),过A作AN⊥PD于N.
 (
( ,2
,2 ,-2
,-2 ),
),
设 ,
,
 =(
=(
 ,2
,2
 ,2
,2 -2
-2
 ).
).  AN⊥PD,
AN⊥PD, 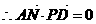 .
.
 ·
·
 +2
+2 ·2
·2
 -2
-2 (2
(2 -2
-2
 )=0.解得
)=0.解得 .
.  ,即
,即 ,同理,过E作EM⊥PD于M,则
,同理,过E作EM⊥PD于M,则 .二面角A-PD-E的大小为
.二面角A-PD-E的大小为 ,
, 所成的角<
所成的角<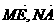 >.
>.  cos<
cos<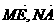 >=
>=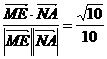 .
. <
<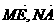 >=arccos
>=arccos  .
. 二面角A-PD-E的大小为arccos
二面角A-PD-E的大小为arccos . ............12分
. ............12分
18、解:(1)由 (n≥1)可得
(n≥1)可得 (n≥2),两式相减得
(n≥2),两式相减得 n+1-
n+1- n=2
n=2 n,
n, .
.
又 2=2S1+1=3,
2=2S1+1=3, ,故{
,故{ n}是首项为1,公比为3的等比数列,
n}是首项为1,公比为3的等比数列,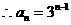 .
............6分
.
............6分
(2)设{ n}的公差为
n}的公差为 ,由T3=15可得
,由T3=15可得 1+
1+ 2+
2+ 3=15,可得
3=15,可得 2=5,故可设
2=5,故可设 1=5-
1=5- ,
, 3=5+
3=5+ .
.
又 1=1,
1=1, 2=3,
2=3, 3=9,由题意可得(5-
3=9,由题意可得(5- +1)(5+
+1)(5+ +9)=(5+3)2,解得
+9)=(5+3)2,解得 1=2,
1=2, 2=-10.
2=-10.
 等差数列{
等差数列{ n}的各项为正,
n}的各项为正,
 =2,
=2, .
.
............12分
17、解:

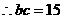 ............3分
............3分


 ............6分
............6分
 b=3 c=5或b=5 c=3
............8分
b=3 c=5或b=5 c=3
............8分
当 b=3 c=5时
b=3 c=5时 
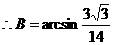 ............10分
............10分
当b=5 c=3时 
 ............12分
............12分
13、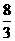 14、19 15、5 16、(1)(3)
14、19 15、5 16、(1)(3)
22.(本小题满分14分)
已知ƒ( )=
)=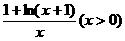 .
.
(1) 函数ƒ( )在区间(0,+
)在区间(0,+ )上是增函数还是减函数?证明你的结论;
)上是增函数还是减函数?证明你的结论;
(2) 当 >0时,证明:ƒ(
>0时,证明:ƒ( )>
)> ;
;
(3) 求证:(1+1·2)(1+2·3)…[1+n(n+1)]>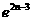
 .
.
2007-2008学年度上学期期末考试高二年级数学科试卷
理科答案
1C 2 B 3 B 4 C 5 C 6 A 7 D 8 D 9 C 10 C 11 C 12 A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com