5．在三维柱形图中，主对角线上两个柱形高度的乘积与副对角线上的两个柱形高度的乘积相差越大，则两个变量有关系的可能性就　 (　 )

A．越大　　　 B．越小　　　 C．无法判断　　　　　 D．以上对不对

4、凡自然数都是整数，而 4是自然数　 所以，4是整数。以上三段论推理(　　 )

　 (A) 正确　　　 　　　　　　　　　　(B)　 推理形式不正确

　 (C)两个“自然数”概念不一致　　　 (D) 两个“整数”概念不一致

3、在两个变量y与x的回归模型中，分别选择了4个不同的模型，它们的相关指数R²如下，其中拟合效果最好的模型是(　　 )

(A)模型1的相关指数R²为0.98　　　　 (B) 模型2的相关指数R²为0.90

(C)模型3的相关指数R²为0.60　　　　 (D) 模型4的相关指数R²为0.25

2. 已知回归直线的斜率的估计值是1.23，样本点的中心为(4，5)，则回归直线的方程是( 　)

　 A.=1.23x+4 　B. =1.23x+5　 C. =1.23x+0.08　　 D. =0.08x+1.23

1、身高与体重有关系可以用(　 )分析来分析

(A)殘差　 　　　　(B)回归　　　　　 (C)二维条形图　　 (D) 独立检验

(二)已知，

①求证：。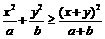

②利用①的结论求的最小值。

21、把边长为60cm的正方形铁皮的四角切去边长为cm的相等的正方形，然后折成一个高度为cm的无盖的长方体的盒子，要求长方体的高度与底面边长的比值不超过常数，

(1)用和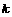表示出长方体的体积的表达式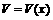，并给出函数的定义域；

(2)问取何值时，盒子的容积最大，最大容积是多少？

22、抛物线方程为y²=p(x+1)(p＞0)，直线x+y=m与x轴的交点在抛物线的准线的右边.

(1)求证：直线与抛物线总有两个交点；

(2)设直线与抛物线的交点为Q、R，OQ⊥OR，

求p关于m的函数f(m)的表达式；

(3)在(2)的条件下，若抛物线焦点F到直线x+y=m的距离为，

求此直线的方程；

莆田四中0007－2008学年上学期

(一)已知，

①求证：；

②若，利用①的结论求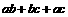的最大值。

17、已知椭圆C的焦点分别为F₁(，0)和F₂(2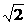，0)，长轴长为6，设直线y=x+2交椭圆C于A、B两点，求椭圆方程和线段AB的中点坐标。

18、已知函数在处有极小值,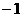

(1)求函数的表达式 ；

(2)求函数的单调递增区间与单调递减区间？

(3)求函数在闭区间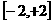上的最大值与最小值？

19、如图，在长方体ABCD-A₁B₁C₁D₁，中，AD=AA₁=1，AB=2，点E在棱AB上移动.

　 (1)证明：D₁E⊥A₁D；

　 (2)AE等于何值时，二面角D₁-EC-D的大小为.

20、选做题，以下两题可任选一题进行作答，若两题都做，则以第一题的得分计算。

16、若三角形的内切圆的半径为，三边长为，则三角形的面积；根据类比的思想，若四面体的内切球的半径为R，四个面的面积为，则四面体的体积＝　　　　 。

15、已知函数在上单调递减，在上单调递增，且函数的导数记为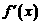，则下列结论正确的命题是　　　 .

① 是方程的根；②1是方程的根；③ 有极小值；

　④有极大值 ； ⑤ 。