6．辆汽车通过某一段公路时的时速的频率分布直方 图如右图所示，时速在的汽车大约有

.辆　　　　　

.辆　

.辆　　　　　

.80辆

5．已知椭圆的焦点是F₁、F₂，P是随圆上的一个动点，如果延长F₁P到Q，使得|PQ|=|PF₂|，　 那么动点Q的轨迹是　

A．圆　　　　 　　B．椭圆　　　　 　　C．双曲线的一支　　　 D．抛物线　　

4．下列命题不正确的是

A　 使用抽签法,每个个体被抽中的机会相等;

B　 使用系统抽样从容量为N的总体中抽取容量为n的样本,确定分段间隔k时，若不是整数,则需随机地从总体中剔除几个个体;

C　 分层抽样就是随意的将总体分成几部分;

D　 无论采取怎样的抽样方法,必须尽可能保证样本的代表性.

3．经过点且与双曲线有共同渐近线的双曲线方程为

A．　　 　　　 B．　　 　　　 C．　　　　　　 D．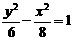

2．有下列四个命题

①“若x+y=0 , 则x ,y互为相反数”的逆命题；

②“全等三角形的面积相等”的否命题；

③“若q≤1 ,则x² + 2x+q=0有实根”的逆否命题；

④“不等边三角形的三个内角相等”逆命题；

其中真命题为　

A．①②　　 　　　　　　　 B．②③　　　　 　　　 　C．①③　　　　 　　 D．③④

1．我校高中生共有2700人,其中高一年级900人,高二年级1200人,现采取分层抽样法抽取容量为135的样本,那么高一、高二、高三各年级抽取的人数分别为

A、45,75,15　 　　　　　 B、 45,45,45 　　　　　　 C、30,90,15　　　 　　　 D、 45,60,30

21、(14分)如图，F₁，F₂分别是椭圆+=1(a﹥b﹥0)的左、右焦点，M为椭圆上一点，MF₂垂直于x轴,且OM与椭圆长轴和短轴端点连线AB平行。

　 (1)求椭圆的离心率；

　 (2)若G为椭圆上不同于长轴端点的任一点，求∠F₁GF₂的取值范围；

　 (3)过F₂且与OM垂直的直线交椭圆于P、Q，若S_△PF1Q=20，求椭圆的方程。

20、(14分)已知P_n(a_n,b_n)都在直线L:y=2x+2上，P₁为直线L与x轴的交点，数列{a_n}是

等差数列，公差为1(n∈N^*)。

(1)求数列{a_n}，{b_n}的通项公式；

　　　　　　　　　 a_n(n为奇数)

(2)若f(n)=　　　　　　　　　 问是否存在k∈N^*,使得f(k+5)=2f(k)-2成立，若存在，

　　　　　　　　　 b_n(n为偶数)

　　　 求出k的值；若不存在，说明理由。

(3)求证：++…+﹤(n≥2,n∈N^*)

19、(14分)如图，正三棱柱ABC-A₁B₁C₁的棱长均为1，D是

CC₁的中点。

　　 (1)求直线AB₁，A₁C所成角的余弦值；

　　 (2)证明：A₁B⊥平面AB₁D；

　　 (3)点A₁到平面AB₁D的距离。

18、(14分)已知双曲线-y²=1,过点P(0,1)作斜率k﹤0的直线L与双曲线恰有一个交点,(1)求直线L的方程；

　　 (2)若点M(x,y)在所有直线L与y=0所围成的平面区域(包括边界)内运动，求Z=-x+y的最小值。