20．点A、B分别是椭圆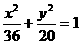长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于轴上方，PA⊥PF，

(1)求点P的坐标；

(2)设M是椭圆长轴AB上的一点，M到直线AP的距离等于|MB|，求椭圆上的点到点M的距离d的最小值.

19．已知双曲线C的中心在原点，抛物线的焦点是双曲线C的一个焦点，且双曲线过点，直线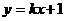：与双曲线C交于A、B两点，

(1)求双曲线的方程；

(2)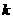为何值时，.

18．统计表明，某种型号的汽车在匀速行驶中每小时的耗油量(升)，关于行驶速度(千米/时)的函数，解析式可以表示为()，已知甲、乙两地相距100千米，

(1)当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

(2)当汽车以多大速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

17．对划船运动员甲、乙两人在相同的条件下进行了6次测试，测得他们最大速度的数据如下：

(1)作出甲、乙数据的茎叶图？(用一幅图表示)

(2)根据以上数据，试判断他们谁更优秀.

16．盒子中只装有4只白球、5只黑球，从中任意取出一只球，

(1)“取出的球是黄球”是什么事件？它的概率是多少？

(2)“取出的球是白球”是什么事件？它的概率是多少？

(3)“取出的球是白球或是黑球”是什么事件，它的概率是多少？

15．设，，……，(，)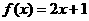

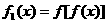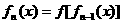　　 求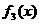，，，…，并由此归纳出的表达式(不需要证明).

14．已知函数，当时，函数取得极大值，当时，函数取得极小值，则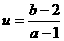取值范围为　　　　　　 .

13．在平面直角坐标系中，已知△ABC的顶点A、C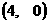，顶点B在椭圆上，则　 　　　　　　．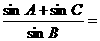

12．设、是椭圆()的两个焦点，P为椭圆上一动点，M为P的中点，P＝4，则OM的长＝　　　　　　 ．

11．函数()的单调递增区间是　　　　　 　　　．