
题目列表(包括答案和解析)
2.设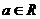 ,则
,则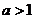 是
是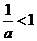 的(
)
的(
)
A.充分不必要条件 B.必要不充分条件 C. 充要条件 D. 不充分也不必要条件
1.设集合 ,则P的子集个数是(
)
,则P的子集个数是(
)
A.3 B.4 C.6 D.8
22.(本小题满分13分)
设x=1和x=2是函数 的两个极值点.
的两个极值点.
(Ⅰ)求 的值;
的值;
(Ⅱ)求 的单调区间.
的单调区间.
成都十八中2007-2008学年度下期高中二年级
21、 (本小题满分13分)
(本小题满分13分)
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=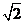 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.
20、 (本小题满分12分)
(本小题满分12分)
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求二面角B-AP-C的大小.
19、(本小题满分12分)
甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加A岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率.
18.(本小题满分12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约.甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率:
(Ⅱ)没有人签约的概率.
17、(本小题满分12分)
已知 展开式中的前三项系数成等差数列,求展开式中含
展开式中的前三项系数成等差数列,求展开式中含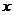 的项
的项
16.若三棱锥的三条侧棱两两垂直,且侧棱长均为 ,则其外接球的表面积是 .
,则其外接球的表面积是 .
15.某高中共有学生1200人,其中高一年级有500人,高二年级有400人,高三年级有300人,采用分层抽样方法抽取一个容量为60的样本,那么高一、高二、高三各年级抽取学生个数分别应为_______________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com