
题目列表(包括答案和解析)
1.命题:“若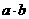 不为零,则
不为零,则 都不为零”的逆否命题是 ▲ 。
都不为零”的逆否命题是 ▲ 。
20.已知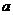 是实数,函数
是实数,函数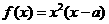 。
。
(Ⅰ)若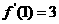 ,求
,求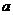 的值及曲线
的值及曲线 在点
在点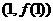 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间 上的最大值。
上的最大值。
解:(Ⅰ) ,
,
因为 ,
,
所以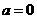 .
.
又当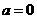 时,
时, ,
, ,
,
所以曲线 在
在 处的切线方程为
处的切线方程为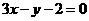 .
.
(Ⅱ)解:令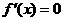 ,解得
,解得 ,
, .
.
当 ,即
,即 时,
时, 在
在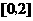 上单调递增,从而
上单调递增,从而
 .
.
当 ,即
,即 时,
时, 在
在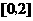 上单调递减,从而
上单调递减,从而
 .
.
当 ,即
,即 时,
时, 在
在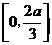 上单调递减,在
上单调递减,在 上单调递增,从而
上单调递增,从而
综上所述, 
19.已知an=4n+5,bn=3n,求证:对任意正整数n,都存在正整数p,使得ap= 成立.
解法一:①当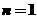 时,
时, ,即存在
,即存在 ,使
,使 ,结论成立;
,结论成立;
②假设当 (
( )时,存在正整数
)时,存在正整数 ,使
,使 ,即
,即 成立.
成立.


∴当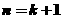 时,存在正整数
时,存在正整数 ,使得
,使得 ,即当
,即当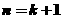 时,结论成立。
时,结论成立。
由①②可得,对 ,存在正整数
,存在正整数 ,使
,使 .
.
法二:∵
 ,
,
又 ,∴
,∴
∴对任意正整数 ,存在
,存在 ,使
,使 。
。
18.已知a+b+c=0且a>b>c。求证: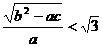
证明:∵a+b+c=0且a>b>c
∴a>0,c<0
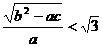

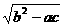 <a
<a
 b2-ac<3a2
b2-ac<3a2
 (-a-c)2-ac<3a2
(-a-c)2-ac<3a2
 2 a2-ac-c2>0
2 a2-ac-c2>0
 (2a+c)(a-c)>0
(2a+c)(a-c)>0
∵a>0,c<0
∴a-c>0
∵a+b+c=0且a>b
∴a>-a-c即2a+c>0
∴(2a+c)(a-c)>0成立
故原不等式得证。
17.某电脑公司有6名产品推销员,其工作年限与年推销金额数据如下表:
|
推销员编号 |
1 |
2 |
3 |
4 |
5 |
工作年限 /年 /年 |
3 |
5 |
6 |
7 |
9 |
推销金额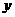 /万元 /万元 |
2 |
3 |
3 |
4 |
5 |
(Ⅰ)求年推销金额 与工作年限x之间的相关系数;
与工作年限x之间的相关系数;
(Ⅱ)求年推销金额 关于工作年限
关于工作年限 的线性回归方程;
的线性回归方程;
(Ⅲ)若第6名推销员的工作年限为11年,试估计他的年推销金额.
(参考数据:;由检验水平0.01及 ,查表得
,查表得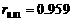 .)
.)
解:
(Ⅰ)由 =10,
=10, 20,
20, 5.2,
5.2,
可得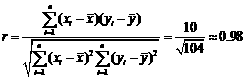 .
.
∴年推销金额 与工作年限x之间的相关系数约为0.98.
与工作年限x之间的相关系数约为0.98.
(Ⅱ) 由(Ⅰ)知, ,
,
∴可以认为年推销金额 与工作年限x之间具有较强的线性相关关系.
与工作年限x之间具有较强的线性相关关系.
设所求的线性回归方程为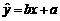 ,
,
则 ,
, .
.
∴年推销金额 关于工作年限
关于工作年限 的线性回归方程为
的线性回归方程为 .
.
(Ⅲ) 由(Ⅱ) 可知,当 时,
时,
 万元.
万元.
∴可以估计第6名推销员的年推销金额为5.9万元.
16.在一次面试中,每位考生从4道题a,b,c,d中任抽两题做,假设每位考生抽到各题的可能性相等,且考生相互之间没有影响.
(1)若甲考生抽到a,b题,求乙考生与甲考生恰好有一题相同的概率;
(2)设某两位考生抽到的题中恰好有X道相同,求随机变量X的概率分布和期望E(X).
解:(1)
答:乙考生与甲考生恰有一题相同的概率为 .
.
(2) 的可能取值为
的可能取值为

 ,
,
所以随机变量 的概率分布为
的概率分布为
|
X |
0 |
1 |
2 |
|
P |
1/6 |
2/3 |
1/6 |
 的期望
的期望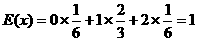
15.已知 为复数,
为复数, .
.
解:设 则
则
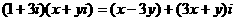
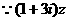 为纯虚数
为纯虚数

于是x=3y 

∴|y|=5 即y=±5
故
14.函数 由下表定义:
由下表定义:
|
x |
1 |
2 |
3 |
4 |
5 |
|
f (x) |
3 |
4 |
5 |
2 |
1 |
若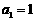 ,
, ,
, 则
则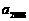 的值________________.1
的值________________.1
13. 如右图,在杨辉三角形中,
如右图,在杨辉三角形中,
从上往下数共有n(n∈N*)行,
在这些数中非1的数字之和为 2n-2n
12、在 的展开式中,含x的系数为
.-9
的展开式中,含x的系数为
.-9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com