
题目列表(包括答案和解析)
20、
解:(Ⅰ)  ,
, 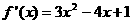
令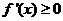 得
得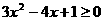 ,解得
,解得
故 的增区间
的增区间 和
和 4分
4分
(Ⅱ)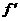 (x)=
(x)=
当x∈[-1,1]时,恒有|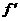 (x)|≤
(x)|≤ . 5分
. 5分
故有 ≤
≤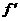 (1)≤
(1)≤ ,
, ≤
≤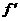 (-1)≤
(-1)≤ ,
,
及 ≤
≤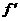 (0)≤
(0)≤ ,
6分
,
6分
即 ………………………8分
………………………8分
①+②,得 ≤
≤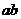 ≤
≤ ,………8分 又由③,得
,………8分 又由③,得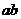 =
= ,将上式代回①和②,得
,将上式代回①和②,得 故
故
 .
10分
.
10分
(Ⅲ)假设 ⊥
⊥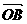 ,即
,即
 =
=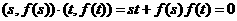 11分
11分
故(s-a)(s-b)(t-a)(t-b)=-1 [st-(s+t)a+a2][st-(s+t)b+b2]=-1,……………11分
由s,t为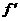 (x)=0的两根可得,s+t=
(x)=0的两根可得,s+t= (a+b), st=
(a+b), st=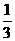 , (0<a<b)
, (0<a<b)
从而有ab(a-b)2=9.………12分
这样
即  ≥2
≥2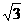 ,这与
,这与 <2
<2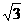 矛盾. ………………………14分
矛盾. ………………………14分
故 与
与 不可能垂直. ………………………16分
不可能垂直. ………………………16分
19、解(1) 定义域为
定义域为 1分
1分
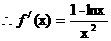 3分
3分
 4分
4分
又
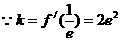 5分
5分
 函数
函数 的在
的在 处的切线方程为:
处的切线方程为:
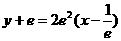 ,即
,即 6分
6分
(2)令 得
得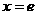
 当
当 时,
时, ,
, 在
在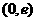 上为增函数
8分
上为增函数
8分
当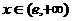 时,
时, ,在
,在 上为减函数
10分
上为减函数
10分
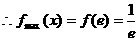 12分
12分
(3)
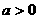 ,由(2)知:
,由(2)知:
 在
在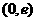 上单调递增,在
上单调递增,在 上单调递减。
上单调递减。

 在
在 上的最小值
上的最小值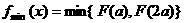 13分
13分
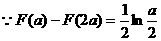 14分
14分
 当
当 时,
时,

 15分
15分
当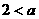 时
时 ,
,
 16分
16分
18、
解:“ 或
或 ”为真命题,则
”为真命题,则 为真命题,或
为真命题,或 为真命题,或
为真命题,或 和
和 都是真命题 3分
都是真命题 3分
当 为真命题时,则
为真命题时,则 ,得
,得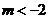 ; 6分
; 6分
当 为真命题时,则
为真命题时,则 9分
9分
当 和
和 都是真命题时,得
都是真命题时,得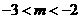 12分
12分
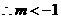 15分
15分
17、
解:设小正方形的边长为 厘米,(0<x<5)
2分
厘米,(0<x<5)
2分
则盒子底面长为 ,宽为
,宽为 (5-2x>0)
4分
(5-2x>0)
4分
 6分
6分
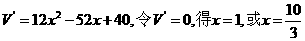 ,
9分
,
9分
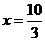 (舍去)
11分
(舍去)
11分
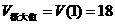 ,在定义域内仅有一个极大值,
14分
,在定义域内仅有一个极大值,
14分
 15分
15分
16、解:假设三个方程: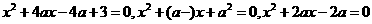 都没有实数根,
都没有实数根,
3分
则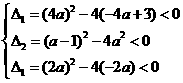 ,
6分
,
6分
即 , 9分
, 9分
得 12分
12分
 。 14分
。 14分
15、解: …………1分
…………1分
若 …………3分
…………3分
若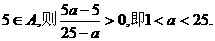 …………5分
…………5分
若 无解; …………8分
无解; …………8分
 …………12分
…………12分
综上,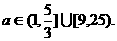 …………14分
…………14分
11、(-2,2) 12、必要条件 13、必要
14、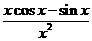
7、 8、
8、 ;
; 9、
9、 10、
10、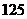
3、①,②,③ 4、①,②,③ 5、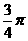 6、
6、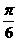
2、存在 且
且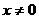 使得
使得 真
真
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com