
题目列表(包括答案和解析)
9.若实数x、y满足 则
则 的取值范围是
( )
的取值范围是
( )
A.(0,2) B.(0,2) C. (2,+∞) D.[2,+∞)
8. 两个圆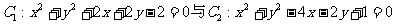 的公切线有且仅有
的公切线有且仅有
A.1条 B.2条 C.3条 D.4条
7. 曲线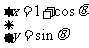 的中心到直线
的中心到直线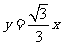 的距离是
( )
的距离是
( )
A.  B.
B.  C.
C.
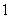 D.
D. 
6. 椭圆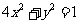 的焦点坐标为
( )
的焦点坐标为
( )
A.  B.
B. 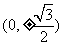 C.
C.  D.
D. 
5. 已知直线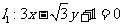 ,直线
,直线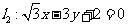 ,则
,则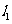 到
到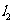 的角
( )
的角
( )
A.  B.
B.  C.
C. 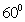 D.
D.
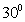
4. 点P从(1,0)出发,沿单位圆 逆时针方向运动
逆时针方向运动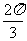 弧长到达Q点,则Q的坐标为
弧长到达Q点,则Q的坐标为
A.  B. (
B. (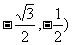 C. (
C. (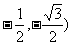 D. (
D. (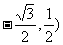
3. 直线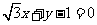 的倾斜角为
( )
的倾斜角为
( )
A. 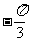 B.
B. 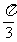 C.
C. 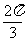 D.
D. 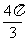
2. 不等式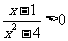 的解集是
( )
的解集是
( )
A
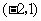 B
B
 C
C
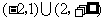 D
D
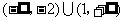
1. a,b两个实数,且a>b,那么一定有 ( )
A. 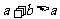 B.
B.  C.
C. 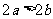 D.
D. 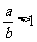
17解: ……………4分
……………4分
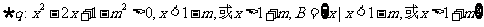 …8分
…8分
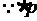 是
是 的必要非充分条件,
的必要非充分条件,

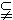
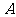 ,即
,即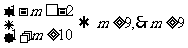 。
…………………………12分
。
…………………………12分
18解:⑴c=2, a=3 双曲线的方程为 …………………………4分
⑵设A(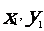 ),B(
),B( )
)
得 (1―3k2)x2―6kx―9=0 ………………………6分
由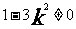 且△>0,得 k2<1且
且△>0,得 k2<1且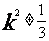 …………8分
…………8分
x1+x2= , x1x2= …………………………………9分
由= x1x2+y1y2=(1+k2) x1x2+k(x1+x2)+2>2得 <k2<3 ………10分
所以,<k2<1 ……………………………………………………11分
即k∈(―1, )∪( , 1 ) … ……………………………………12分
19 解:(1)8道题中任抽2道题的方法有28种,其中两道都在不会答的3道题中抽出的方法有3种,故他及格的概率=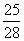 。
………………………4分
。
………………………4分
(2)如果他会3道题,则两道都不会答的方法有10种,及格的概率 ,仍大于
,仍大于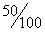 。
……………………………………………………8分
。
……………………………………………………8分
当他只会2道题时,抽到2道题都不会的方法数为15种,此时他及格的概率=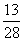 小于
小于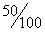
 ,即他最多会2题。
………………………12分
,即他最多会2题。
………………………12分
20解:(1)由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小,
因此第二小组的频率为: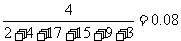 ………………………2分
………………………2分
又因为频率=
所以  ………………………4分
………………………4分
(2)由图可估计该学校高一学生的达标率约为
 ………………………8分
………………………8分
(3)由已知可得各小组的频数依次为6,12,51,45,27,9,所以前三组的频数之和为69,前四组的频数之和为114,所以跳绳次数的中位数落在第四小组内。 ……12分
21解.(I)这是计算1+3+5+…+101结果的流程图
流程图(2)、(3)判断框中的条件分别是:(2)I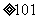 (I>100)
(I>100)
(3) I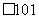 …………6分
…………6分
(II)若交换三个流程图中S←S+I与I←I+2的位置,则:
(1)第二个处理框中改为 S←1,判断框条件改为I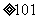 …………9分
…………9分
(2) 第二个处理框中改为 S←1,判断框条件改为I>101 …………12分
(3) 第二个处理框中改为 S←1,判断框条件改为I<101 …………15分
22解.⑴设P(x0, y0)为圆C上任意一点,Q(x, y)的横坐标与P相同,纵坐标为P的一半,
即x0= x, y0=2y ……………………………………………………………………2分
又P(x0, y0)满足x02+y02 = 4 则x2+4y2 = 4 ………………………………………4分
即 求曲线C的方程为 ……………………………………………6分
⑵当l的斜率不存在时,、 AB=3都不成立; ………………………7分
当l的斜率存在时,设斜率为k,
则A、B两点的坐标(x1, y1)、(x2,y2)是方程组的解
整理,得:(1+4k2)x2―8k2x+12k2―4 =0
x1+x2=, x1x2= …………………………………………………9分
∴N的坐标为xN = ,yN= k(xN-) =
∴ON的方程为y= x
与C的方程联立,得 ………………………………11分
必要性(→AB=3):由得 =2× =2 xN
∴ k2= …………………………………………………………………12分
此时 AB=…=a-ex1+a-ex2=2a-e(x1+x2)=4-×=3
∴充分性成立 ……………………………………………………………13分
充分性(AB=3→):
AB=…=a-ex1+a-ex2=2a-e(x1+x2)=4-×=3
∴ k2=
∴ = ,xN = = ……………………14分
∴ xE =2 xN 又E、N共线
∴必要性成立……………………………………15分
综上,的充要条件是AB=3.………………………………………16分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com