4、满足b=1, c=3, 且焦点在y轴上的椭圆方程是　　　　　 。

3、椭圆的两个焦点坐标分别为F₁(-3，0)，F₂(3，0)，P是椭圆上任意一点，且PF₁+PF₂=2F₁F₂

,则椭圆的标准方程是　　　　　　　　 。

2、椭圆4x² + y ² = 16的离心率为　　　　 。

21.(14分) 已知圆 　和圆外一点M ( 4，- 8 )．

　　　 (Ⅰ) 过M作圆的切线，切点为C、D，求切线长及CD所在直线的方程；

　　　 (Ⅱ) 过M作圆的割线交圆于A，B两点，若| AB | = 4，求直线AB的方程．

　麻 城 博 达 学 校 2008 年 高 二 数 学 同 步 测 试 (03)

20.(13分)北京某商厦计划同时出售新款空调和洗衣机．由于这两种产品的市场需求量大，供不应求，因此该商厦要根据实际情况(生产成本、运输费等)确定产品的月供应量，以使得总利润达到最大．通过调查，得到经销这两种产品的有关数据如下表：

　　 试问：怎样确定这两种产品的月供应量，才能使总利润达到最大，且最大利润是多少？

19.(12分)已知直线l：x+y－2＝0，一束光线从点P(0，1+)以120°的倾斜角射到直线l上反

　 射，求反射光线所在的直线方程．

17.(12分) 已知一个圆截y轴所得的弦为2，被x轴分成的两段弧长的比为3∶1.(1)设圆心

　 (a，b)，求实数a，b满足的关系式；(2)当圆心到直线l：x－2y＝0的距离最小时，求圆的方

　 程．

⒙　　 (12分)已知圆C的圆心在直线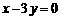上，且圆C与y轴相切，若圆C截直线得弦长为，求圆C的方程．

16.(12分) 设M是圆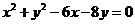上的动点，O是原点，N是射线OM上的点，若

　 ，求点N的轨迹方程。

15.若圆x²+y²=r²(r>0)上恰有相异的两点到直线4x－3y+25=0的距离等于1，则r的取值范围

　 是　 　　　　　　　．

14. 设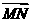的起点在曲线C₁：上，终点在曲线C₂：

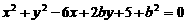　 上，则当实数a、b变化时，的取值范围是_______________