20.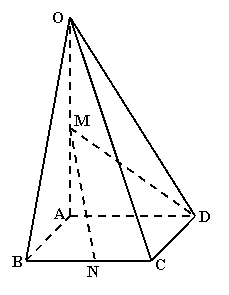如图，在四棱锥O-ABCD中，底面ABCD是边长

为1的菱形，∠ABC=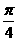，OA⊥底面ABCD，OA=2，

M为OA的中点，N为BC的中点。

(1)　　　 证明：直线MN∥平面OCD；

(2)　　　 求异面直线AB与MD所成角的大小；

(3)　　　 求点B到平面OCD的距离。

19.已知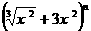展开式各项系数的和比它的二项式系数的和大992。

(1)　　　 求n；

(2)　　　 求展开式中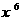的项；

(3)　　　 求展开式系数最大项。

18. 甲乙等五名大冬会志愿者被随机的分到A，B，C，D四个不同的岗位服务，每岗位至少有一名志愿者。

(1)　 共有多少中不同的安排方法；

(2)　 求甲乙两人同时参加A岗位服务的概率；

(3)　 求甲乙两人不在同一岗位服务的概率。

17. 从1，2，…，10这10个数字中有放回的抽取三次，每次抽取一个数字。

(1)取出的三个数字全不同的概率；

(2)三次抽取中最小数为3的概率。

16.将红、黄、蓝三种颜色涂到3×3的方格中，要求每行每列都没有重复颜色，则不同的涂色方法共有　　　种。

三 解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤，写在答题纸的相应位置)

15.正三棱柱内有一个内切球，已知球的半径为R，则这个正三棱柱的底面边长为　　　　　 。

14. 某单位安排小张、小王、小李、小赵和小刘轮流值班，每人值一天，并且始终按照小张、小王、小李、小赵、小刘的顺序，今天是小赵值班，则再过天值班人是　 　　　　　。

13. 将红、黄、蓝三种颜色涂到3×3的方格中，要求每行每列都没有重复颜色，则不同的涂色方法共有　　　种。

12. 在的展开式中，含的偶次幂的项之和为S，当时，S等于　 (　　　 )

A. 　　　　　B. 　　　　　　C. 　　　　　　D.

第Ⅱ卷(非选择题 共90分)

11. 在边长为1的菱形ABCD中，∠ABC=60^O，将菱形沿对角线AC折起，使折起后BD=1，则二面角B-AC-D的余弦值为　　　　　　　　　　　　 　　　　　　　　　　　　　(　　　 )

A. 　　　　　　B.　　　　　　　 C.　　　　　　 D.