
题目列表(包括答案和解析)
5、若原命题“ ”,则其逆命题、否命题、逆否命题中( D )
”,则其逆命题、否命题、逆否命题中( D )
A、都真 B、都假 C、否命题真 D、逆否命题真
4、如果双曲线的半实轴长为2,焦距为6,那么该双曲线的离心率是 ( C )
A、 B、
B、 C、
C、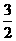 D、2
D、2
3.椭圆的焦距为2,则m的值等于 ( A )
A.5或3 B.8 C.5 D. 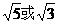
2.“p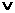 q为真”是“
q为真”是“ p为假”的
( B)
p为假”的
( B)
A.充分不必要条件. B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
1.已知命题 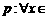 R,
R, ,则( C
)
,则( C
)
A.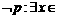 R,
R, 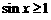 B.
B. R,
R, 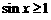
C.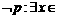 R,
R, 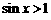 D.
D. R,
R, 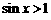
20.已知函数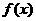 和
和 的图象关于原点对称,且
的图象关于原点对称,且
⑴求函数 的解析式;
的解析式;
⑵解不等式 ≥
≥
⑶若 在[-1,1]上为增函数,求实数
在[-1,1]上为增函数,求实数 的取值范围.
的取值范围.
命题、校对:凌卫红
19.已知圆C的方程为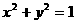 ,直线
,直线 过点A(3,0),且与圆C相切.
过点A(3,0),且与圆C相切.
⑴求直线 的方程.
的方程.
⑵设圆C与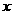 轴相交于
轴相交于 ,
,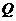 两点,M是圆C上异于
两点,M是圆C上异于 ,
,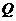 的任意一点,过点A且与
的任意一点,过点A且与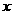 轴垂直的直线为
轴垂直的直线为 ,直线PM交直线
,直线PM交直线 于点
于点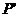 ,直线
,直线 交直线
交直线 于点
于点 ,求证以
,求证以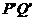 为直径的圆
为直径的圆 总经过定点,并求出定点坐标.
总经过定点,并求出定点坐标.
18.2008年“三聚氰胺”事件给中国的牛奶制造业带来了巨大的冲击,为保障人民的饮食安全,国家质检部门把查处的问题奶集中进行无害化处理,某单位承担了本地区问题奶的处理任务,在国家科研部门的支持下,该单位经过科技攻关,采用了新工艺,把问题奶转化为一种可利用的化工产品,每吨可获利2万元,已知该单位每月可处理7-12吨,其处理成本 (万元)与月处理量
(万元)与月处理量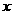 (吨)之间的函数关系式可近似地表示为:
(吨)之间的函数关系式可近似地表示为:
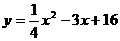 ,问:
,问:
⑴该单位每月处理多少吨时,才能使每吨的处理成本最低?并求出最低成本;
⑵该单位能否获得利润?如果不能,则国家需补贴多少才能使该单位不亏损?如果能,求出最大利润.
17.已知 的一个顶点
的一个顶点 ,直线
,直线 ,若
,若 分别是边
分别是边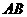 、
、 上的中线,求
上的中线,求 边所在直线方程.
边所在直线方程.
16.如图,在四棱锥O-ABCD中,底面ABCD是菱形,OA⊥平面ABCD,E为OA的中点,F为BC的中点,求证:
⑴平面BDO⊥平面ACO;
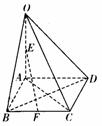 ⑵直线EF∥平面OCD.
⑵直线EF∥平面OCD.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com