
题目列表(包括答案和解析)
5、设f(n)>0(n∈N*),且f(2)=4,对任意n1、n2∈N*有f(n 1+n 2)= f(n 1)+ f(n 2)恒成立,则猜想f(n)的一个表达式为( **)
A、f(n)= n 2 B、f(n)= n + 2 C、f(n)= 2 n D、f(n)= 2 n
4、若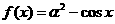 ,则
,则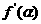 等于
( *)
等于
( *)
A、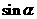 B、
B、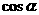 C、
C、 D、
D、 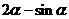
3、用反证法证明命题“三角形的内角中至少有一个不大于60°”时,反设正确的是( )
A、假设三个内角都不大于60° B、假设三个内角都大于60°
C、假设三个内角至多有一个大于60° D、假设三个内角至多有两个大于60°
2、过抛物线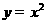 上一点P
上一点P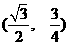 的切线的倾斜角是 ( )
的切线的倾斜角是 ( )
A、90° B、60° C、45° D、30°
1、已知复数
z 满足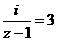 ,则复数 z为
( )
,则复数 z为
( )
A、1+3i
B、 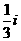 C、
C、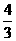 D、
D、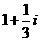
22.(本小题满分14分)如图,在长方体ABCD─A1B1C1D1中,E、P分别是BC、A1D1的中点,M、N分别是AE、CD1的中点,AD=AA1=a,AB=2a.
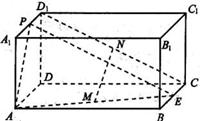 (1)求证:MN∥面ADD1A1;
(1)求证:MN∥面ADD1A1;
(2)求二面角P─AE─D的大小;
(3)求三棱锥P─DEN的体积.
本资料由《七彩教育网》 提供!
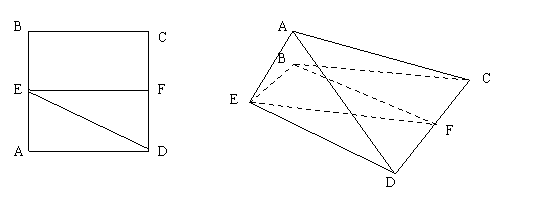
21.(本小题满分12分)已知正方形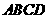 .
.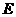 、
、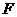 分别是
分别是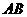 、
、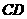 的中点,将ADE沿
的中点,将ADE沿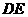 折起,如图所示,记二面角
折起,如图所示,记二面角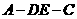 的大小为
的大小为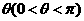 .
.
(1)证明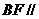 平面
平面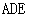 ;
;
(2)若△ACD为正三角形,试判断点 在平面
在平面 内的射影
内的射影 是否在直线
是否在直线 上,证明你的结论,并求角
上,证明你的结论,并求角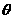 的余弦值.
的余弦值.

20.(本小题满分12分)(理)如图,已知矩形ABCD,PA⊥平面ABCD,M、N分别是AB、PC的中点,设AB=a,BC=b,PA=c.
(1)建立适当的空间直角坐标系,写出A、B、M、N点的坐标,并证明MN⊥AB;
(2)平面PDC和平面ABCD所成的二面角为θ,当θ为何值时(与a、b、c无关), MN是直线AB和PC的公垂线段.
MN是直线AB和PC的公垂线段.
(文)正方体ABCD-A1B1C1D1中,M、N、P分别为棱AB、
BC、DD1的中点.
(1)求证:PB⊥平面MNB1;
(2)设二面角M-B1N-B为α,求cosα的值.
19.(本小题满分12分)已知二面角a-a-b等于60°,点P为这个二面角内一点,作PA⊥a,PB⊥b,垂足分别为A、B,若PA=1,PB=2,求点P到棱a的距离
18.(本小题满分12分)A是△BCD所在平面外的点,∠BAC=∠CAD=∠DAB=60°,AB=3,AC=AD=2.
(Ⅰ)求证:AB⊥CD;
(Ⅱ)求AB与平面BCD所成角的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com