
题目列表(包括答案和解析)
4. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球半径为 )( )
)( )
 .
.
 .
. 
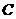 .
.
 .
. 
3. 集合 中元素个数为( )
中元素个数为( )
 .2个
.2个
 .3个
.3个 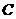 .4个
.4个
 .5个
.5个
2.  展开式中,二项式系数最大的项是( )
展开式中,二项式系数最大的项是( )
 .第n-1项
.第n-1项  .第n项
.第n项
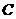 .第n-1项与第n+1项
.第n-1项与第n+1项  .第n项与第n+1项
.第n项与第n+1项
1. 将四名教师分配到三个班级去参加活动,要求每班至少一名的分配方法有( )
 .72种
.72种  .48种
.48种 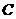 .36种
.36种  .24种
.24种
20.(本小题满分10分)
已知双曲线的焦点在x轴上,两渐近线方程为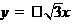 ,点A、B在双曲线上,且关于直线 x+y+2=0对称,|AB|=
,点A、B在双曲线上,且关于直线 x+y+2=0对称,|AB|=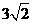 .
.
(Ⅰ)求线段AB的中点C的坐标;
(Ⅱ)求这双曲线的方程;
(Ⅲ)过点(0,1)作直线l与双曲线的左、右两支分别相交于P、Q两点,点M(0,-1)为定点,试推断是否存在直线l,使 ?若存在,求直线l的方程;若不存在,说明理由.
?若存在,求直线l的方程;若不存在,说明理由.
[解](Ⅰ)设双曲线方程为3x2-y2=λ(λ>0),点A(x1,y1),B(x2,y2),C(x0,y0),则
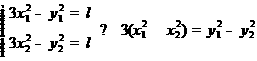 ,即3(x1-x2)(x1+x2)=(y1-y2)(y1+y2). (1分)
,即3(x1-x2)(x1+x2)=(y1-y2)(y1+y2). (1分)
因为点A、B关于直线x+y+2=0对称,所以 ,即
,即 .
.
又C为AB的中点,所以x1+x2=2x0,y1+y2=2y0. 于是有3x0=y0. (2分)
因为点C在直线x+y+2=0上,所以x0+y0+2=0.
于是4 x0+2=0,即 ,从而
,从而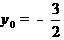 ,故点
,故点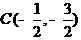 .
(3分)
.
(3分)
(Ⅱ)因为|AB|=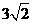 ,所以|AC|=
,所以|AC|= ,于是
,于是 ,即x1=1. (4分)
,即x1=1. (4分)
又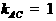 ,即
,即 ,所以
,所以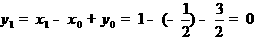 .
(5分)
.
(5分)
因为点A(1,0)在双曲线上,所以λ=3x12-y12=3.故双曲线方程是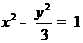 . (6分)
. (6分)
(Ⅲ)设直线l的方程为y=kx+1,代入双曲线方程,得 ,
,
即  .
(7分)
.
(7分)
设点P(x3,y3),Q(x4,y4),则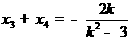 ,
,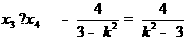 . (8分)
. (8分)
因为 ,
,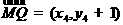 .
.
所以
 .
(9分)
.
(9分)
因为P、Q分别为双曲线左、右两支上的点,则 .
.
所以 .故不存在直线l,使
.故不存在直线l,使 .
(10分)
.
(10分)
本资料由《七彩教育网》 提供!
19.(本小题满分8分)
 如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=1,∠BAC=90°,试用向量方法解决下列问题.
如图,在直三棱柱ABC-A1B1C1中,AB=AC=AA1=1,∠BAC=90°,试用向量方法解决下列问题.
(Ⅰ)求点C1到平面AB1C的距离;
(Ⅱ)求二面角A1-B1C-A的大小.
[解](Ⅰ)因为AA1⊥平面ABC, AB⊥AC,分别以AB,
AC,AA1为x轴,y轴,z轴,建立空间直角坐标系. (1分)
因为AB=AC=AA1=1,则点C(0,1,0),B1(1,0,1),
C1(0,1,1),所以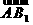 =(1,0,1),
=(1,0,1), =(0,1,0).
(2分)
=(0,1,0).
(2分)
设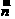 =(x,y,z)为平面AB1C的法向量,则
=(x,y,z)为平面AB1C的法向量,则
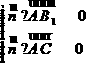 ,即
,即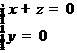 . 取x=1,则
. 取x=1,则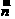 =(1,0,-1). (3分)
=(1,0,-1). (3分)
又 =(0,0,-1),故点C1到平面AB1C的距离
=(0,0,-1),故点C1到平面AB1C的距离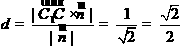 .
(4分)
.
(4分)
(Ⅱ)因为点A1(0,0,1),所以 =(0,-1,1),
=(0,-1,1), =(1,-1,1). (5分)
=(1,-1,1). (5分)
设 =(x,y,z)为平面A1B1C的法向量,则
=(x,y,z)为平面A1B1C的法向量,则
 ,即
,即 .取z=1,则
.取z=1,则 =(0,1,1). (6分)
=(0,1,1). (6分)
因为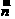 =(1,0,-1),则
=(1,0,-1),则 ,
,
所以 . (7分)
. (7分)
由图知,二面角A1-B1C-A的平面角为锐角,故二面角A1-B1C-A的大小为60°. (8分)
18.(本小题满分8分)
 已知椭圆中心在原点,焦点在x轴上,点F1、F2分别为椭圆的左、右焦点,点P为椭圆上一点.若椭圆的离心率为
已知椭圆中心在原点,焦点在x轴上,点F1、F2分别为椭圆的左、右焦点,点P为椭圆上一点.若椭圆的离心率为 ,且△PF1F2的周长为16.
,且△PF1F2的周长为16.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆左顶点作直线l,若动点M到椭圆右焦点的距离
比它到直线l的距离小4,求点M的轨迹方程.
[解](Ⅰ)设椭圆的半长轴长为a,半短轴长为b,半焦距为c,
则|PF1|+|PF2|=2a,|F1F2|=2c. (1分)
因为△PF1F2的周长为16,即|PF1|+|PF2|+|F1F2|=16,所以2a+2c=16,即a+c=8.(2分)
又 ,即a=3c,从而4c=8,所以c=2,a=6,b2=a2-c2=36-4=32.
(3分)
,即a=3c,从而4c=8,所以c=2,a=6,b2=a2-c2=36-4=32.
(3分)
因为椭圆的焦点在x轴上,故椭圆的标准方程是 .
(4分)
.
(4分)
(Ⅱ)法一:因为a=6,所以直线l的方程为x=-6,又c=2,所以右焦点为F2(2,0). (5分)
过点M作直线l的垂线,垂足为H,由题设,|MF2|=|MH|-4.
设点M(x,y),则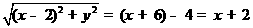 .
(6分)
.
(6分)
两边平方,得 ,即y2=8x.
(7分)
,即y2=8x.
(7分)
故点M的轨迹方程是y2=8x. (8分)
法二:因为a=6,c=2,所以a-c=4,从而椭圆左焦点F1到直线l的距离为4. (5分)
由题设,动点M到椭圆右焦点的距离与它到直线x=-2的距离相等,所以点M的轨迹是以右焦点为F2(2,0)为焦点,直线x=-2为准线的抛物线. (7分)
显然抛物线的顶点在坐标原点,且p=|F1F2|=4,故点M的轨迹方程是y2=8x. (8分)
17.(本小题满分8分)
在空间直角坐标系中,已知三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(Ⅰ)求〈 〉的大小;
〉的大小;
(Ⅱ)设直线AB与坐标平面xOy的交点为D,求C,D两点间的距离.
[解](Ⅰ)由已知,得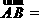 (-2,-1,3),
(-2,-1,3),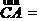 (-1,3,-2).
(1分)
(-1,3,-2).
(1分)
则 2―3―6=-7.
2―3―6=-7.  .
(2分)
.
(2分)
所以cos〈 〉=
〉= .
(3分)
.
(3分)
故〈 〉=120°.
(4分)
〉=120°.
(4分)
(Ⅱ)设点D(x,y,0),则 (x,y-2,-3).
(5分)
(x,y-2,-3).
(5分)
因为向量 与
与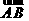 共线,设
共线,设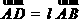 ,则(x,y-2,-3)=λ(-2,-1,3). (6分)
,则(x,y-2,-3)=λ(-2,-1,3). (6分)
于是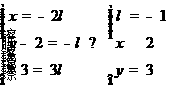 ,所以点D(2,3,0). (7分)
,所以点D(2,3,0). (7分)
故 ,即C,D两点间的距离是
,即C,D两点间的距离是 . (8分)
. (8分)
16.(本小题满分6分)
已知含有量词的两个命题p和q,其中命题p:任何实数的平方都大于零;命题q:二元一次方程2x+y=3有整数解.
(Ⅰ)用符号“ ”与“
”与“ ”分别表示命题p和q;
”分别表示命题p和q;
(Ⅱ)判断命题“(﹁p)∧q”的真假,并说明理由.
[解](Ⅰ)命题p: x∈R,x2>0;
(1分)
x∈R,x2>0;
(1分)
命题q: x0∈Z且y0∈Z,2x0+y0=3.
(3分)
x0∈Z且y0∈Z,2x0+y0=3.
(3分)
(Ⅱ)因为当x=0时,x2=0,所以命题p为假命题,从而命题﹁p为真命题. (4分)
因为当x0=2,y0=-1时,2x0+y0=3,所以命题q为真命题. (5分)
故命题“(﹁p)∧q”是真命题. (6分)
15.已知动点M分别与两定点A(1,0),B(-1,0)的连线的斜率之积为定值m(m≠0),若点M的轨迹是焦点在x轴上的椭圆(除去点A、B),则m的取值范围是(-1,0);若点M的轨迹是离心率为2的双曲线(除去点A、B),则m的值为 3 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com