
题目列表(包括答案和解析)
 的最大值为2.
的最大值为2. ,角A,B,C所对的边分别是a,b,c,且C=60°,c=3,求△ABC的面积.
,角A,B,C所对的边分别是a,b,c,且C=60°,c=3,求△ABC的面积. 的最大值为2.
的最大值为2.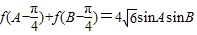 ,角A,B,C所对的边分别是a,b,c,且C=60°,c=3,求△ABC的面积.
,角A,B,C所对的边分别是a,b,c,且C=60°,c=3,求△ABC的面积.已知函数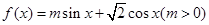 的最大值为2.
的最大值为2.
(Ⅰ)求函数 在
在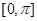 上的单调递减区间;
上的单调递减区间;
(Ⅱ)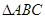 中,
中, ,角
,角 所对的边分别是
所对的边分别是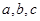 ,且
,且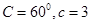 ,求
,求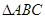 的面积.
的面积.
 的最大值为2.
的最大值为2. 在
在 上的单调递减区间;
上的单调递减区间; 中,
中, ,角
,角 所对的边分别是
所对的边分别是 ,且
,且 ,求
,求 的面积.
的面积.
说明:
一、本解答给出一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题
的主要考查内容比照评分标准制订相应的评分细则.
二、对计算题当考生的解答在某一步出现错误时,如果后续部分的解答未改变该题的
内容和难度,可视影响的程度决定给分,但不得超过该部分正确解答应得分数的一
半;如果后续部分的解答有较严重的错误,就不再给分.
三、解答右端所注分数,表示考生正确做到这一步应得累加分.
四、只给整数分数,选择题和填空题不给中间分数.
一、选择题(每小题5分,满分60分)
1.C 2.C 3.B 4.D 5.D 6.B 7.A 8.D 9.B 10.B 11.C 12. A
简答与提示:
1.程组可得交点 ,故选C
,故选C
2.正弦定理可知“ ” 是使“
” 是使“ ”成立的充要条件。故选C
”成立的充要条件。故选C
3. 。故选B
。故选B
4. 因为四个命题均有线在面内的可能,所以均不正确,故选D
5. 故选D
故选D
6.以 为直径的圆与圆
为直径的圆与圆 的公共弦即为所求,直线方程为
的公共弦即为所求,直线方程为 ,故
,故
选B.
7.将 的图像先向左平移
的图像先向左平移 个单位得到
个单位得到 的图像,再沿
的图像,再沿 轴将横坐标
轴将横坐标
压缩到原来的 倍(纵坐标不变)得到
倍(纵坐标不变)得到 的图像,故选A
的图像,故选A
8.在点 处目标函数取得最大值为-1,故选D.
处目标函数取得最大值为-1,故选D.
9.先在后三位中选两个位置填两个数字“ 种填法,再排另两张卡片有
种填法,再排另两张卡片有 种排法,
种排法,
再决定用数字“ 个四位数,故选B.
个四位数,故选B.
10.

 最大,也可用赋值法,
最大,也可用赋值法, 代入即可,故选B
代入即可,故选B
11.
 ,当
,当 三点共线时取得最小值,故选C
三点共线时取得最小值,故选C
12.因为函数 在其定义域内为减函数,所以
在其定义域内为减函数,所以
 恒成立,即
恒成立,即 为减函数(切线斜率减小),故选A
为减函数(切线斜率减小),故选A
13. 14.
14. 15.9 16.①②④
15.9 16.①②④
简答与提示:
13.设正方体棱长为 ,则
,则
14.∵ ,∴
,∴ ,∴
,∴ .
.
15.
16.由 知函数
知函数 关于点
关于点 对称,且可得
对称,且可得 ,由
,由
 知函数
知函数 关于
关于 轴对称,进一步可推出周期为4,所以
轴对称,进一步可推出周期为4,所以
 ,故①②④正确
,故①②④正确
三、解答题(满分70分)
17.本小题主要考查三角函数的基本公式、三角恒等变换、三角函数图象及性质.
解:(1)∵

∴ .
.
(2)当 ,即
,即 时,
时, , ,
, ,
当 ,即
,即 ,
, ,
,
∴函数 的值域为[
的值域为[ ,1].
,1].
18.(1)本小题主要考查概率的基本知识与分类思想,考查运用数学知识分析问题解决问题
的能力.
解.(1)中一等奖的概率为 ,
,
中二等奖的概率为 ,
,
中三等奖的概率为 ,
,
∴摇奖一次中奖的概率为
(2)由(1)可知,摇奖一次不中奖的概率为
两次摇奖庄家获利包括两次均未中奖和一次未中奖一次中三等奖两种情况,
所以庄家获利的概率为:
19.本小题主要考查空间线面位置关系、异面直线所成角、二面角等基本知识,考查空间想
象能力、逻辑思维能力和运算能力以及空间向量的应用.
解法一:
(1)证明:
取 中点为
中点为 ,连结
,连结 、
、 ,
,
 ∵△
∵△ 是等边三角形,
是等边三角形,
∴
又∵侧面
 底面
底面 ,
,
∴ 底面
底面 ,
,
∴ 为
为 在底面
在底面 上的射影,
上的射影,
又∵ ,
,
 ,
,
∴ ,
,
∴ ,
,
∴ ,
,
∴ .
.
(2)取 中点
中点 ,连结
,连结 、
、 ,
,
∵ .
.
∴ .
.
又∵ ,
, ,
,
∴ 平面
平面 ,
,
∴
 ,
,
∴ 是二面角
是二面角 的平面角.
的平面角.
∵ ,
, ,
,
∴ .
.
∴ ,
,
∴ ,
,
∴ ,
,
∴二面角 的大小为
的大小为
解法二:证明:(1) 取 中点为
中点为 ,
, 中点为
中点为 ,连结
,连结 ,
,
∵△ 是等边三角形,
是等边三角形,
∴ ,
,
又∵侧面
 底面
底面 ,
,
∴ 底面
底面 ,
,
∴以 为坐标原点,建立空间直角坐标系
为坐标原点,建立空间直角坐标系
如图, (2分)
∵ ,△
,△ 是等边三角形,
是等边三角形,
 ∴
∴ ,
,
∴ .
.
∴ .
.
∵
∴ .
.
(2)设平面 的法向量为
的法向量为
∵
∴
令 ,则
,则 ,∴
,∴
设平面 的法向量为
的法向量为 ,
,
∵ ,
,
∴ ,
,
令 ,则
,则 ,∴
,∴
∴ ,
,
∴ ,
,
∴二面角 的大小为
的大小为 .
.
20.本小题主要考查函数的单调性、极值等基本知识,考查运用导数研究函数性质的方法,
函数与方程思想,考查分析问题和解决问题的能力。
解:(1)

(2)

 方程
方程 有3个不等实根
有3个不等实根
 函数
函数 的图像与
的图像与 轴有三个不同的交点
轴有三个不同的交点

21.本小题主要考查等差数列定义、通项、数列求和、不等式等基础知识,考查综合分析问
题的能力和推理论证能力。
解:(1)

 数列
数列 是以2为首项,以1为公差的等差数列。
是以2为首项,以1为公差的等差数列。

(3)

22. 本小题主要考查直线、椭圆等平面解析几何的基础知识,考查轨迹的求法以及综合解
题能力
解:(1)设 ,则
,则
∵ ,∴
,∴ ,∴
,∴ ,
,
又 ,∴
,∴
∴曲线 的方程为
的方程为
(2)由(1)可知, (4,0)为椭圆
(4,0)为椭圆 的右焦点,设直线
的右焦点,设直线 方程为
方程为
 ,由
,由 消去
消去 得,
得, ,
,
∴
∴
 ,
,
当 ,即
,即 时取得最大值,
时取得最大值,
此时直线方程为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com