练习册

  • 练习册
  • 试题
    19． 据调查.某地区100万从事传统农业的农民.人均收入3000元.为了增加农民的收入.当地政府积极引进资本.建立各种加工企业.对当地的农产品进行深加工.同时吸收当地部分农民进入加工企业工作.据估计.如果有x万人进企业工作.那么剩下从事传统农业的农民的人均收入有望提高2x%.而进入企业工作的农民的人均收入为3000a元.(I)在建立加工企业后.要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入.试求x的取值范围,的条件下.当地政府应该如何引导农民.能使这100万农民的人均年收入达到最大. 【查看更多】

     

    题目列表(包括答案和解析)

    （2011•广东模拟）（本小题满分14分 已知函数f(x)=
    		3
    sin2x+2sin(
    π
    4
    +x)cos(
    π
    4
    +x)    ．
    （I）化简f（x）的表达式，并求f（x）的最小正周期；
    （II）当x∈[0，
    π
    2
    ]  时，求函数f(x)    的值域．

    查看答案和解析>>

    （本小题满分14分）已知的图像在点处的切线与直线平行.

    ⑴ 求，满足的关系式；

    ⑵ 若上恒成立，求的取值范围；

    ⑶ 证明：（）

     

    查看答案和解析>>

    (本小题满分14分) 设是定义在区间上的偶函数，命题：在上单调递减；命题：，若“或”为假，求实数的取值范围。

    查看答案和解析>>

    （07年安徽卷文）（本小题满分14分）设F是抛物线G:x2=4y的焦点.

    　　　（Ⅰ）过点P（0，-4）作抛物线G的切线，求切线方程：

    （Ⅱ）设A、B为势物线G上异于原点的两点，且满足,延长AF、BF分别交抛物线G于点C,D，求四边形ABCD面积的最小值.

    查看答案和解析>>

    (本小题满分14分)关于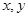的方程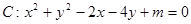

    （1）若方程C表示圆，求实数m的取值范围；

    （2）在方程C表示圆时，若该圆与直线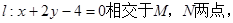

    且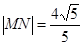，求实数m的值；

    （3）在（2）的条件下，若定点A的坐标为（1，0），点P是线段MN上的动点，

    求直线AP的斜率的取值范围。

     

    查看答案和解析>>

    一．选择题：CBBA  CAAA

    二．填空题：9、；  10、 ；  11、；12、； 

    13、； 14、；  15、

    三．解答题：

    16．解：（I）tanC＝tan[π－（A＋B）]＝－tan（A＋B）

                ∵， ∴       ……………………5分

    （II）∵0<tanB<tanA，∴A、B均为锐角, 则B<A，又C为钝角，

    ∴最短边为b ，最长边长为c……………………7分

    由，解得       ……………………9分

    由    ，∴       ………………12分

    17.解：（I）“油罐被引爆”的事件为事件A，其对立事件为，则P()=C…………4分

    ∴P(A)=1-         答：油罐被引爆的概率为…………6分

    （II）射击次数ξ的可能取值为2，3，4，5，    …………7分

           P(ξ=2)=，   P(ξ=3)=C     ，

    P(ξ=4)=C， P(ξ=5)=C …………10分

    ξ

    2

    3

    4

    5

            故ξ的分布列为：

                                                                                             

     

    Eξ=2×+3×+4×+5×=   …………12分

    18．解（Ⅰ）当n = 1时，解出a1 = 3 , …………1分

    又4sn = an2 + 2an－3                             ①

            当时    4sn－1 =  + 2an-1－3                             ②  

                ①－②  , 即…………3分

    ∴ ,（）…………5分

    是以3为首项，2为公差的等差数列   …………7分

    （Ⅱ）                               ③

    又              ④    …………9 分

    ④－③       …………11分

                       …………13分

                                     …………14分

    19. 解：（I）由题意得（100-x）?3000?（1+2x%）≥100×3000，

    即x2－50x≤0，解得0≤x≤50，                        ……………………4分

    又∵x＞0   ∴0＜x≤50；                            ……………………6分

    （II）设这100万农民的人均年收入为y元，

    则y=  =

    =－[x－25(a+1)]2+3000+475(a+1)2     (0<x≤50)    ………………9分

    （i）当0<25(a+1)≤50，即0＜a≤1，当x=25(a+1)时，y最大； ………………11分

    （ii）当25(a+1)＞50，即a ＞1，函数y在（0,50]单调递增，∴当x=50时，y取最大值。…………13分                          

    答：在0＜a≤1时，安排25(a +1)万人进入企业工作，在a＞1时安排50万人进入企业工作，才能使这100万人的人均年收入最大             ………………14分

    20．解证：（I）易得…………………………………………1分

    的两个极值点，的两个实根，又＞0

    ……………………………………………………3分

    ∴

    ∵，

                ……………………………………………7分

    （Ⅱ）设则

    由   ………………10分

    ∴在上单调递增；在上单调递减………………12 分

    ∴时，取得极大值也是最大值

    ，………………………………………14分

    22．（本小题满分14分）

    解：（I）由图形可知二次函数的图象过点（0，0），（8，0），并且f(x)的最大值为16

    则，

    ∴函数f（x）的解析式为…………………………4分

    （Ⅱ）由得

    ∵0≤t≤2，∴直线l1与f（x）的图象的交点坐标为（…………………………6分

    由定积分的几何意义知：

    ………………………………9分

    （Ⅲ）令

    因为x＞0，要使函数f（x）与函数g（x）有且仅有2个不同的交点，则函数

    的图象与x轴的正半轴有且只有两个不同的交点

    ∴x=1或x=3时，

    当x∈（0，1）时，是增函数；

    当x∈（1，3）时，是减函数

    当x∈（3，+∞）时，是增函数

    ∴……………12分

    又因为当x→0时，；当

    所以要使有且仅有两个不同的正根，必须且只须

    即， ∴m=7或

    ∴当m=7或时，函数f（x）与g（x）的图象有且只有两个不同交点。…………14分

     


    同步练习册答案