
题目列表(包括答案和解析)
一自来水厂用蓄水池通过管道向所管辖区域供水.某日凌晨,已知蓄水池有水9千吨,水厂计划在当日每小时向蓄水池注入水2千吨,且每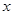 小时通过管道向所管辖区域供水
小时通过管道向所管辖区域供水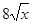 千吨.
千吨.
(1)多少小时后,蓄水池存水量最少?
(2)当蓄水池存水量少于3千吨时,供水就会出现紧张现象,那么当日出现这种情况的时间有多长?
【解析】第一问中(1)设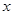 小时后,蓄水池有水
小时后,蓄水池有水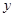 千吨.依题意,
千吨.依题意, 当
当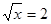 ,即
,即 (小时)时,蓄水池的水量最少,只有1千吨
(小时)时,蓄水池的水量最少,只有1千吨
第二问依题意,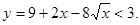 解得:
解得:
解:(1)设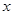 小时后,蓄水池有水
小时后,蓄水池有水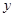 千吨.………………………………………1分
千吨.………………………………………1分
依题意, …………………………………………4分
…………………………………………4分
当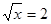 ,即
,即 (小时)时,蓄水池的水量最少,只有1千吨. ………2分
(小时)时,蓄水池的水量最少,只有1千吨. ………2分
(2)依题意,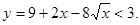 ………………………………………………3分
………………………………………………3分
解得: . …………………………………………………………………3分
. …………………………………………………………………3分
所以,当天有8小时会出现供水紧张的情况
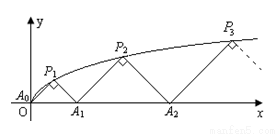
如图,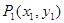 ,
,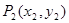 ,…,
,…,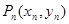 ,…是曲线
,…是曲线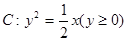 上的点,
上的点,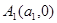 ,
,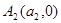 ,…,
,…, ,…是
,…是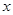 轴正半轴上的点,且
轴正半轴上的点,且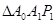 ,
,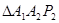 ,…,
,…, ,…
均为斜边在
,…
均为斜边在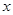 轴上的等腰直角三角形(
轴上的等腰直角三角形( 为坐标原点).
为坐标原点).
(1)写出 、
、 和
和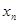 之间的等量关系,以及
之间的等量关系,以及 、
、 和
和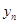 之间的等量关系;
之间的等量关系;
(2)求证: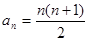 (
(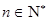 );
);
(3)设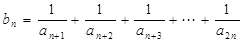 ,对所有
,对所有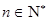 ,
,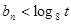 恒成立,求实数
恒成立,求实数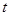 的取值范围.
的取值范围.
【解析】第一问利用有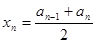 ,
,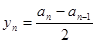 得到
得到
第二问证明:①当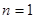 时,可求得
时,可求得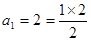 ,命题成立;②假设当
,命题成立;②假设当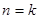 时,命题成立,即有
时,命题成立,即有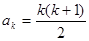 则当
则当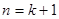 时,由归纳假设及
时,由归纳假设及 ,
,
得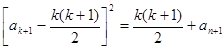
第三问
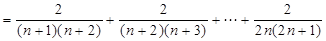
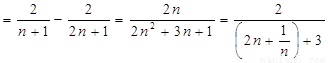 .………………………2分
.………………………2分
因为函数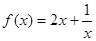 在区间
在区间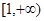 上单调递增,所以当
上单调递增,所以当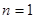 时,
时,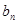 最大为
最大为 ,即
,即
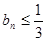
解:(1)依题意,有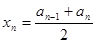 ,
,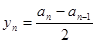 ,………………4分
,………………4分
(2)证明:①当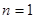 时,可求得
时,可求得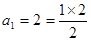 ,命题成立;
……………2分
,命题成立;
……………2分
②假设当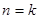 时,命题成立,即有
时,命题成立,即有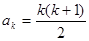 ,……………………1分
,……………………1分
则当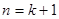 时,由归纳假设及
时,由归纳假设及 ,
,
得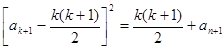 .
.
即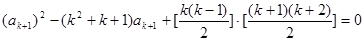
解得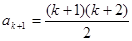 (
(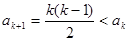 不合题意,舍去)
不合题意,舍去)
即当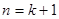 时,命题成立. …………………………………………4分
时,命题成立. …………………………………………4分
综上所述,对所有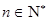 ,
,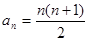 . ……………………………1分
. ……………………………1分
(3)
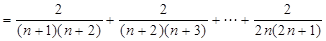
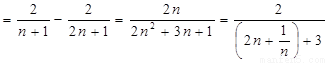 .………………………2分
.………………………2分
因为函数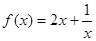 在区间
在区间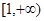 上单调递增,所以当
上单调递增,所以当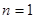 时,
时,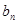 最大为
最大为 ,即
,即
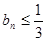 .……………2分
.……………2分
由题意,有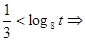
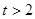 .
所以,
.
所以,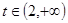
已知数列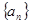 的前
的前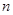 项的和为
项的和为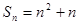 ,
,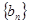 是等比数列,且
是等比数列,且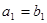 ,
,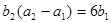 。
。
⑴求数列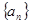 和
和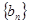 的通项公式;
的通项公式;
⑵设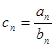 ,求数列
,求数列 的前
的前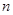 项的和
项的和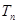 。
。
⑴  ,数列
,数列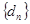 的前
的前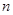 项的和为
项的和为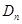 ,求证:
,求证: .
.
【解析】第一问利用数列
依题意有:当n=1时,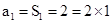 ;
;
当 时,
时,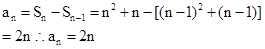
第二问中,利用由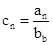 得:
得: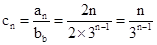 ,然后借助于错位相减法
,然后借助于错位相减法
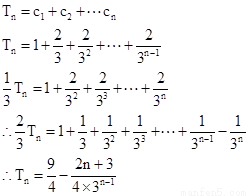
第三问中
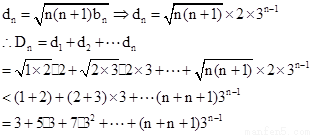
结合均值不等式放缩得到证明。
在 中,已知
中,已知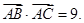
 ,面积
,面积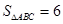 ,
,
(1)求 的三边的长;
的三边的长;
(2)设 是
是 (含边界)内的一点,
(含边界)内的一点, 到三边
到三边 的距离分别是
的距离分别是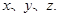
①写出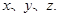 所满足的等量关系;
所满足的等量关系;
②利用线性规划相关知识求出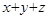 的取值范围.
的取值范围.
【解析】第一问中利用设 中角
中角 所对边分别为
所对边分别为
由 得
得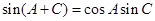

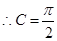
又由 得
得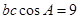 即
即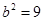

又由 得
得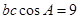 即
即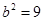

又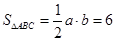
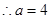 又
又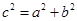 得
得
即 的三边长
的三边长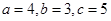

第二问中,①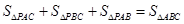 得
得
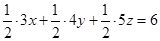
故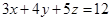
②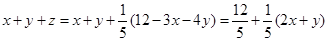
令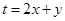 依题意有
依题意有
作图,然后结合区域得到最值。

某村计划建造一个室内面积为 的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留
的矩形蔬菜温室。在温室内,沿左、右两侧与后侧内墙各保留 宽的通道,沿前侧内墙保留
宽的通道,沿前侧内墙保留 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
【解析】本试题考查了实际生活中的最值问题的运用,首先确定设矩形温室的长为xm,则宽为800/xm。
依题意有:种植面积:
运用导数的思想得到最值。
设矩形温室的长为xm,则宽为800/xm。
依题意有:种植面积:

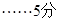
答:当矩形温室的长为20m,宽为40m时种植面积最大,最大种植面积是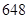 m2
m2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com