
题目列表(包括答案和解析)
已知 ,函数
,函数
(1)当 时,求函数
时,求函数 在点(1,
在点(1, )的切线方程;
)的切线方程;
(2)求函数 在[-1,1]的极值;
在[-1,1]的极值;
(3)若在 上至少存在一个实数x0,使
上至少存在一个实数x0,使 >g(xo)成立,求正实数
>g(xo)成立,求正实数 的取值范围。
的取值范围。
【解析】本试题中导数在研究函数中的运用。(1)中 ,那么当
,那么当 时,
时, 又
又  所以函数
所以函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 ;(2)中令
;(2)中令 有
有 

对a分类讨论 ,和
,和 得到极值。(3)中,设
得到极值。(3)中,设 ,
, ,依题意,只需
,依题意,只需 那么可以解得。
那么可以解得。
解:(Ⅰ)∵ ∴
∴ 
∴ 当 时,
时, 又
又 
∴ 函数 在点(1,
在点(1, )的切线方程为
)的切线方程为 --------4分
--------4分
(Ⅱ)令 有
有 

①
当 即
即 时
时
|
|
(-1,0) |
0 |
(0, |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
极大值 |
|
极小值 |
|
故 的极大值是
的极大值是 ,极小值是
,极小值是
②
当 即
即 时,
时, 在(-1,0)上递增,在(0,1)上递减,则
在(-1,0)上递增,在(0,1)上递减,则 的极大值为
的极大值为 ,无极小值。
,无极小值。
综上所述  时,极大值为
时,极大值为 ,无极小值
,无极小值
 时 极大值是
时 极大值是 ,极小值是
,极小值是 ----------8分
----------8分
(Ⅲ)设 ,
,
对 求导,得
求导,得
∵ ,
,

∴  在区间
在区间 上为增函数,则
上为增函数,则
依题意,只需 ,即
,即
解得  或
或 (舍去)
(舍去)
则正实数 的取值范围是(
的取值范围是(
 ,
, )
)
已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式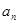 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当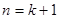 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
已知向量 夹角为
夹角为 ,且
,且 ;则
;则
【解析】因为 ,所以
,所以 ,即
,即 ,所以
,所以 ,整理得
,整理得 ,解得
,解得 或
或 (舍去).
(舍去).
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
|
|
视觉记忆能力 |
||||
|
偏低 |
中等 |
偏高 |
超常 |
||
|
听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
|
中等 |
1 |
8 |
3 |
|
|
|
偏高 |
2 |
|
0 |
1 |
|
|
超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为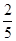 .
.
(I)试确定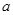 、
、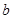 的值;
的值;
(II)从40人中任意抽取3人,求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率;
(III)从40人中任意抽取3人,设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为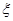 ,求随机变量
,求随机变量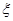 的数学期望
的数学期望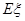 .
.
【解析】1)中由表格数据可知,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的学生共有(10+a)人.记“视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上”为事件A,则P(A)=(10+a)/40=2/5,解得a=6.……………2分
所以.b=40-(32+a)=40-38=2答:a的值为6,b的值为2.………………3分
(2)中由表格数据可知,具有听觉记忆能力或视觉记忆能力超常的学生共有8人.
方法1:记“至少有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件B,
则“没有一位具有听觉记忆能力或视觉记忆能力超常的学生”为事件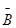
(3)中由于从40位学生中任意抽取3位的结果数为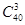 ,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为
,其中具有听觉记忆能力或视觉记忆能力偏高或超常的学生共24人,从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的结果数为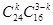 ,………………………7分
,………………………7分
所以从40位学生中任意抽取3位,其中恰有k位具有听觉记忆能力或视觉记忆能力偏高或超常的概率为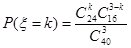 ,k=0,1,2,3
,k=0,1,2,3
已知幂函数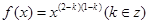 满足
满足 。
。
(1)求实数k的值,并写出相应的函数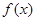 的解析式;
的解析式;
(2)对于(1)中的函数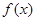 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数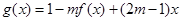 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数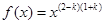 满足
满足 ,得到
,得到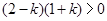
因为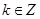 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为
(2)由(1)知,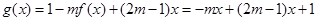 ,
, ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: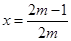 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到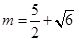
(1)对于幂函数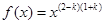 满足
满足 ,
,
因此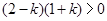 ,解得
,解得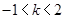 ,………………3分
,………………3分
因为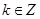 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时, ,
,
当k=1时, ,综上所述,k的值为0或1,
,综上所述,k的值为0或1, 。………………6分
。………………6分
(2)函数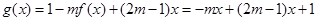 ,………………7分
,………………7分
由此要求 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: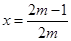 ,
,
当 时,
时,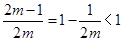 ,因为在区间
,因为在区间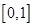 上的最大值为5,
上的最大值为5,
所以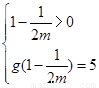 ,或
,或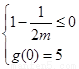 …………………………………………10分
…………………………………………10分
解得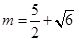 满足题意
满足题意
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com