
题目列表(包括答案和解析)
【例】
已知函数y=sin2x+![]() cos2x-2.
cos2x-2.
(1)用“五点法”作出函数在一个周期内的图象;
(2)求这个函数的周期和单调区间;
(3)求函数图象的对称轴方程.
(4)说明图象是由y=sinx的图象经过怎样的变换得到的.
![]() 学科网
学科网
某乡为提高当地群众的生活水平,由政府投资兴建了甲、乙两个企业,2007年该乡从甲企业获得利润320万元,从乙企业获得利润720万元.以后每年上交的利润是:甲企业以1.5倍的速度递增,而乙企业则为上一年利润的![]() .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
(1)若以2007年为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题?
(2)试估算2015年底该乡能否达到小康水平?为什么?
【解题思路】经审题抽象出数列模型
【例】 如右图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+![]() )+B.
)+B.
(1)求这段时间的最大温差;
(2)写出这段曲线的函数解析式.
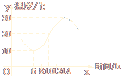
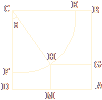
【例】某体育馆拟用运动场的边角地建一个矩形的健身室.如图所示,ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在![]() 上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在
上.设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在![]() 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com