
题目列表(包括答案和解析)
(本小题满分13分)
如图在直三棱柱ABC—A1B1C1中,AC=BC=2,AA1=![]() ,∠ACB=90°,M是AA1的中点,N是BC1的中点。
,∠ACB=90°,M是AA1的中点,N是BC1的中点。
(1)求证:MN∥平面A1B1C1
|
(3)求二面角B-C1M—A的大小.
(本小题满分13分)
如图,在直三棱柱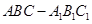 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中, 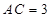 ,
,
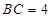 ,
,
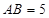 ,
,
 ,点
,点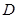 是
是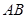 的中点.
的中点.

(Ⅰ)
求证: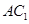 ∥平面
∥平面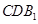 ;
;
(Ⅱ)求AC1与平面CC1B1B所成的角.
(本小题满分13分)
如图,在直三棱柱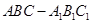 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中,  ,
, 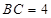 ,
, 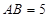 ,
,  ,点
,点 是
是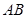 的中点.
的中点. 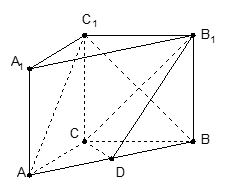
(Ⅰ) 求证: ∥平面
∥平面 ;
;
(Ⅱ)求AC1与平面CC1B1B所成的角.
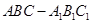 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中,  ,
,  ,
,  ,
,  ,点
,点 是
是 的中点.
的中点. 
 ∥平面
∥平面 ;
;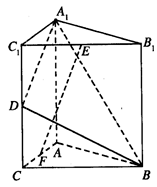 (本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(本小题满分13分)如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB. D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
一、选择题:本大题每小题5分,满分50分.
1
2
3
4
5
6
7
8
9
10
C
A
A
C
B
A
B
D
D
B
二、填空题:本大题共5小题,每小题5分,满分20分,其中14,15题是选做题,考生只能选做一题,,若两题全都做的,只计算前一题的得分.
11.(2,+∞) 12.试题.files/image298.gif) 13. 4 14.
13. 4 14.试题.files/image300.gif) 15. 9
15. 9
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
解:(Ⅰ)∵
试题.files/image302.gif) , ………………1分
, ………………1分
(Ⅱ)由试题.files/image310.gif) 且
且试题.files/image312.gif) ,…………………7分
,…………………7分
试题.files/image320.gif) 17.(本小题满分13分)
17.(本小题满分13分)
证明: (1) ∵ 三棱柱试题.files/image205.gif) 为直三棱柱,
为直三棱柱,
∴ 试题.files/image322.gif) 平面
平面试题.files/image324.gif) , ∴
, ∴试题.files/image326.gif) ,
,
∵ 试题.files/image207.gif) ,
, 试题.files/image209.gif) ,
, 试题.files/image211.gif) ,
,
∴ 试题.files/image328.gif) ,
,
∴ 试题.files/image330.gif) , 又
, 又 试题.files/image332.gif) ,
,
∴ 试题.files/image334.gif) 平面
平面试题.files/image336.gif) ,
,
∴ 试题.files/image217.gif) ……………………………………7分
……………………………………7分
(2) 令试题.files/image338.gif) 与
与试题.files/image340.gif) 的交点为
的交点为试题.files/image122.gif) , 连结
, 连结试题.files/image343.gif) .
.
∵ 试题.files/image182.gif) 是
是试题.files/image126.gif) 的中点,
的中点, 试题.files/image122.gif) 为
为试题.files/image338.gif) 的中点, ∴
的中点, ∴ 试题.files/image343.gif) ∥
∥试题.files/image219.gif) .
.
又 ∵试题.files/image219.gif)
试题.files/image347.gif) 平面
平面试题.files/image221.gif) ,
, 试题.files/image343.gif)
试题.files/image350.gif) 平面
平面试题.files/image221.gif) ,
,
∴试题.files/image219.gif) ∥平面
∥平面试题.files/image221.gif) . ………………………13分
. ………………………13分
18.(本小题满分13分)
解: (1) 由题意得 试题.files/image352.gif) , 即
, 即 试题.files/image354.gif) ,…………………1分
,…………………1分
当试题.files/image356.gif) 时 ,
时 , 试题.files/image358.gif) ,…………4分
,…………4分
当试题.files/image360.gif) 时,
时, 试题.files/image362.gif) , ………………5分
, ………………5分
∴ 试题.files/image364.gif) , ……………………6分
, ……………………6分
(2) 由(1)得试题.files/image366.gif) ,…………………8分
,…………………8分
∴ 试题.files/image368.gif)
试题.files/image370.gif) . ……………………11分
. ……………………11分
因此,使得试题.files/image372.gif) 成立的
成立的试题.files/image108.gif) 必须且只需满足
必须且只需满足试题.files/image374.gif) , 即
, 即试题.files/image376.gif) ,
,
故满足要求的的最小正整数试题.files/image378.gif) ………………13分
………………13分
19.(本小题满分14分)
解: (1)设圆试题.files/image177.gif) 的圆心为
的圆心为试题.files/image380.gif) ,
,
依题意圆的半径 试题.files/image382.gif) ……………… 2分
……………… 2分
∵ 圆试题.files/image177.gif) 在
在试题.files/image159.gif) 轴上截得的弦
轴上截得的弦试题.files/image250.gif) 的长为
的长为试题.files/image252.gif) .
.
∴ 试题.files/image384.gif)
故 试题.files/image386.gif) …………………………
4分
…………………………
4分
∴
试题.files/image388.gif)
∴ 圆试题.files/image177.gif) 的圆心的轨迹方程为
的圆心的轨迹方程为试题.files/image388.gif) ………………… 6分
………………… 6分
(2) ∵
试题.files/image254.gif) , ∴
, ∴ 试题.files/image390.gif) ……………………… 9分
……………………… 9分
令圆试题.files/image177.gif) 的圆心为
的圆心为试题.files/image392.gif) , 则有
, 则有试题.files/image394.gif) (
(试题.files/image396.gif) ) ,…………… 10分
) ,…………… 10分
又
∵ 试题.files/image398.gif) …………………… 11分
…………………… 11分
∴ 试题.files/image400.gif) ……………………… 12分
……………………… 12分
∴ 试题.files/image402.gif) ………………………
13分
………………………
13分
∴ 圆试题.files/image177.gif) 的方程为
的方程为 试题.files/image404.gif) …………………… 14分
…………………… 14分
21.(本小题满分14分)
解:(Ⅰ)由已知试题.files/image406.gif)
解得试题.files/image289.gif) ,
,试题.files/image409.gif) ,
…………………2分
,
…………………2分
∴ 试题.files/image411.gif) , ∴
, ∴ 试题.files/image413.gif) …………4分
…………4分
∴ 试题.files/image415.gif) . ……………………5分
. ……………………5分
(Ⅱ)在(Ⅰ)条件下,试题.files/image268.gif) 在区间
在区间试题.files/image270.gif) 恒成立,即
恒成立,即试题.files/image417.gif) 在区间
在区间试题.files/image270.gif) 恒成立,
恒成立,
从而试题.files/image419.gif) 在区间
在区间试题.files/image270.gif) 上恒成立,…………………8分
上恒成立,…………………8分
令函数试题.files/image422.gif) ,
,
则函数试题.files/image422.gif) 在区间
在区间试题.files/image270.gif) 上是减函数,且其最小值
上是减函数,且其最小值试题.files/image425.gif) ,
,
∴ 试题.files/image272.gif) 的取值范围为
的取值范围为试题.files/image428.gif) …………………………10分
…………………………10分
(Ⅲ)由试题.files/image276.gif) ,得
,得试题.files/image431.gif) ,
,
∵
试题.files/image433.gif) ∴
∴试题.files/image435.gif) ,………………11分
,………………11分
设方程试题.files/image437.gif) 的两根为
的两根为试题.files/image439.gif) ,则
,则试题.files/image441.gif) ,
,试题.files/image443.gif) ,
,
∴试题.files/image445.gif) ,
,
∵
试题.files/image281.gif) , ∴
, ∴ 试题.files/image447.gif) , ∴
, ∴试题.files/image449.gif) ,
,
∵
试题.files/image433.gif) 且
且试题.files/image452.gif) , ∴
, ∴ 试题.files/image454.gif) ,
,
∴
试题.files/image456.gif) ……………14分
……………14分
21.(本小题满分14分)
解: (Ⅰ)解:当试题.files/image289.gif) 时,
时,试题.files/image459.gif) ,
,试题.files/image461.gif) ,……………1分
,……………1分
又试题.files/image463.gif) ,则
,则试题.files/image465.gif) .…………………3分
.…………………3分
所以,曲线试题.files/image291.gif) 在点
在点试题.files/image293.gif) 处的切线方程为
处的切线方程为试题.files/image469.gif) ,
,
即试题.files/image471.gif) .……………4分
.……………4分
(Ⅱ)解:试题.files/image473.gif) .…………6分
.…………6分
由于试题.files/image295.gif) ,以下分两种情况讨论.
,以下分两种情况讨论.
(1)当试题.files/image433.gif) 时,令
时,令试题.files/image477.gif) ,得到
,得到试题.files/image479.gif) ,
,试题.files/image481.gif) ,
,
当试题.files/image159.gif) 变化时,
变化时,试题.files/image484.gif) 的变化情况如下表:
的变化情况如下表:
试题.files/image159.gif)
试题.files/image487.gif)
试题.files/image489.gif)
试题.files/image491.gif)
试题.files/image063.gif)
试题.files/image494.gif)
试题.files/image496.gif)
试题.files/image498.gif)
0
试题.files/image500.gif)
0
试题.files/image498.gif)
试题.files/image260.gif)
试题.files/image504.gif)
极小值
试题.files/image506.gif)
极大值
试题.files/image504.gif)
所以试题.files/image260.gif) 在区间
在区间试题.files/image509.gif) ,
,试题.files/image511.gif) 内为减函数,在区间
内为减函数,在区间试题.files/image513.gif) 内为增函数
内为增函数
故函数试题.files/image260.gif) 在点
在点试题.files/image479.gif) 处取得极小值
处取得极小值试题.files/image517.gif) ,且
,且试题.files/image519.gif) ,
,
函数试题.files/image260.gif) 在点
在点试题.files/image481.gif) 处取得极大值
处取得极大值试题.files/image523.gif) ,且
,且试题.files/image525.gif) .…………………10分
.…………………10分
(2)当试题.files/image527.gif) 时,令
时,令试题.files/image477.gif) ,得到
,得到试题.files/image530.gif) ,
,
当试题.files/image159.gif) 变化时,
变化时,试题.files/image484.gif) 的变化情况如下表:
的变化情况如下表:
试题.files/image159.gif)
试题.files/image533.gif)
试题.files/image063.gif)
试题.files/image536.gif)
试题.files/image489.gif)
试题.files/image539.gif)
试题.files/image496.gif)
试题.files/image500.gif)
0
试题.files/image498.gif)
0
试题.files/image500.gif)
试题.files/image260.gif)
试题.files/image506.gif)
极大值
试题.files/image504.gif)
极小值
试题.files/image506.gif)
所以试题.files/image260.gif) 在区间
在区间试题.files/image542.gif) ,
,试题.files/image543.gif) 内为增函数,在区间
内为增函数,在区间试题.files/image544.gif) 内为减函数.
内为减函数.
函数试题.files/image260.gif) 在
在试题.files/image546.gif) 处取得极大值
处取得极大值试题.files/image523.gif) ,且
,且试题.files/image525.gif) .
.
函数试题.files/image260.gif) 在
在试题.files/image550.gif) 处取得极小值
处取得极小值试题.files/image517.gif) ,且
,且试题.files/image519.gif) .………………14分
.………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com