
题目列表(包括答案和解析)
(本小题满分12分)
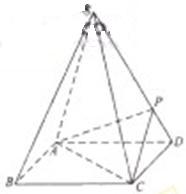
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的![]() 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E, 使得BE∥平面PAC。若存在,求SE:EC的值;若不存在,试说明理由。
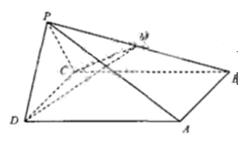
(本小题满分12分)如图,四棱锥![]() 中,侧面PDC是边长为2的正三角形,且与底面
中,侧面PDC是边长为2的正三角形,且与底面![]() 垂直,底面ABCD是面积为
垂直,底面ABCD是面积为![]() 的菱形,
的菱形,![]() 为锐角,M为PB的中点。
为锐角,M为PB的中点。
(1)求证![]()
(2)求二面角![]() 的大小
的大小
(3)求P到平面![]() 的距离
的距离
(本小题满分12分)
如图,四棱锥P—ABCD中,平面PAD⊥平面ABCD,AB//CD,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4![]() 。
。
(I)设M是PC上的一点,证明:平面MBD⊥平面PAD。
(II)求四棱锥P—ABCD的体积。
 (本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(1) 求异面直线AF与BG所成的角的大小;
(2) 求平面APB与平面CPD所成的锐二面角的大小.
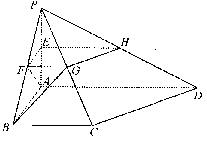 (本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(本小题满分12分)如图,四棱锥P-ABCD中,PA⊥平面ABCD,PA=AB=BC=2,E为PA的中点,过E作平行于底面的平面EFGH,分别与另外三条侧棱相交于点F、G、H. 已知底面ABCD为直角梯形,AD∥BC,AB⊥AD,∠BCD=135°.
(1) 求异面直线AF与BG所成的角的大小;
(2) 求平面APB与平面CPD所成的锐二面角的大小.
一、选择题: CCBCD DCDBB C A
二、填空题: 13.
45 14. 30 15.  16.
16. 
三、解答题:17.解: (1)  ………1分
………1分

 ,化简得
,化简得 …3分
…3分

(2) )
)

令 Z),函数f(α)的对称轴方程为
Z),函数f(α)的对称轴方程为 Z).……12分
Z).……12分
18.解:(1)油罐没被引爆分两种情形:
①5发子弹只有1发击中,其概率为:
②5发子弹全没有击中,其概率为

(2) 的可能取值为2,3,4,5.
的可能取值为2,3,4,5.

∴ 的分布列为:
的分布列为:

2
3
4
5
P




 的数学期望为:E
的数学期望为:E =2×
=2× +3×
+3× +4×
+4× +5×
+5× =
= .……………………12分
.……………………12分
19. (1)证明:∵PA⊥底面ABCD,∴PA⊥AD.又AB⊥BC,PA∩AB=A,∴BC⊥平面PAB.……(3分) 又BC 平面PCB,∴平面PAB⊥平面PCB.……5分
平面PCB,∴平面PAB⊥平面PCB.……5分
(2)解:过A作AF∥BC,交CD于F,以A为原点,AF,AB,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系Axyz.
设PA=AB=BC=a,则A(0,0,0), B(0,a,0),C(a,a,0), P(0,0,a), E(0, 

 .……………………………………8分
.……………………………………8分
设n1=(x,y,1)为平面AEC的一个法向量, 则n1⊥ ,n1⊥
,n1⊥ ,
,
∴ 解得x=
解得x= , y=-
, y=- ,∴n1=(
,∴n1=( ,-
,- ,1).
,1).
设n2=(x′,y′,1)为平面PBC的一个法向量,同理可得n2=(0,1,1).…………11分
cos<n1,n2>= =
= ∴平面AEC和平面PBC所成锐二面角的余弦值为
∴平面AEC和平面PBC所成锐二面角的余弦值为 .…12分
.…12分
20. 解:(1)由an+1=2an+n+1可得an+1+(n+1)+2=2(an+n+2),
所以数列{an+n+2}是一个公比为2的等比数列,其首项为a1+1+2=-1+1+2=2,
于是an+n+2=2?2n-1=2n.…………(10分) 故an=2n-n-2.
{an}的前n项和Sn= ……6分
……6分
(2)证明:假设{an}是等比数列,设其首项为a1,
则a2=2a1+2,
a3=2a2+3=4a1+7,………(8分)于是有(2a1+2)2=a1(4a1+7),解得:a1=-4,于是公比 ,这时a4=a1q3=(-4)×(
,这时a4=a1q3=(-4)×( )3=-
)3=- .…………………10分
.…………………10分
但是由题中所给递推公式,a4=2a3+4=8a1+18=-14,二者矛盾,所以{an}不可能是等比数列.……………………12分
21.解:(1)设椭圆C的方程为 半焦距为c,依题意有
半焦距为c,依题意有
|PF|=|F1F2|=2c
∴ 解得
解得 ,∴b=1. ∴所求椭圆方程为
,∴b=1. ∴所求椭圆方程为 …4分
…4分
(2)由 得
得 .
.
设点A、B的坐标分别为A(x1, y1)、B(x2,y2), ……………………6分
……………………6分
 .
.
①当m=0时,点A、B关于原点对称,则λ=0.②当m≠0时,点A、B不关于原点对称,则λ≠0.

∵点Q在椭圆上,∴有 ……………8分
……………8分
化简得4m2(1+2k2)=
 ∵
∵
∵直线与椭圆交于不同的两点,△=16k2m2-4(1+2k2)(2m2-2)=8(2k2+1-m2) ∴ (1+2k2-m2)>0,
1+2k2>m2.(**)…(10分)由(*)(**)可得4m2> .∵m≠0, ∴
.∵m≠0, ∴
综上,实数 的取值范围是(-2,2).………………………………………12分
的取值范围是(-2,2).………………………………………12分
22.解:(1)函数f(x)的定义域为:(-∞, -1)∪(-1, +∞),……………………1分
∵ …………………………………2分
…………………………………2分
令 令
令 得x<-2或-1<x<0.
得x<-2或-1<x<0.
则函数f(x)的递增区间是(-2,-1), (0, +∞),递减区间是(-∞, -2), (-1, 0).………4分
(2)由(1)知,f(x)在[ 上递减,在[0,e-1]上递增,又
上递减,在[0,e-1]上递增,又

 ,故m> e2-2时,不等式恒成立.……8分
,故m> e2-2时,不等式恒成立.……8分
(3)依题意,原命题等价于方程x-a+1-ln(1+x)2=0在x∈[0, 2]上有两个相异的实根,……9分
记h(x)=x-a+1-ln(1+x)2, 则h′(x)=1- 令h′(x)>0,得x<-1或x>1,令h′(x)<0,得-1<x<1.
令h′(x)>0,得x<-1或x>1,令h′(x)<0,得-1<x<1.
∴h(x)在[0, 1)上递减,在(1,2]上递增.………………10分
为使h(x)在[0,2]上恰好有两个相异的实根,只须h(x)=0在[0,1)和(1,2]上各有一个实根,于是有 即a的取值范围是(2-ln2, 3-ln3].…………14分
即a的取值范围是(2-ln2, 3-ln3].…………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com