
题目列表(包括答案和解析)
如图,椭圆中心在原点,F为左焦点,当![]() ⊥
⊥![]() 时其离心率为
时其离心率为![]() ,此类椭圆被称为“黄金椭圆”.
,此类椭圆被称为“黄金椭圆”.
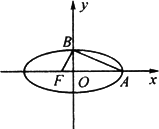
(1)类比“黄金椭圆”,可推算出“黄金双曲线”的离心率等于多少?(只要写出结论即可)
(2)已知椭圆E:![]() 的一个焦点f(c,0)(c>0),试证:若a,b,c不是等比数列,则E一定不是“黄金椭圆”.
的一个焦点f(c,0)(c>0),试证:若a,b,c不是等比数列,则E一定不是“黄金椭圆”.
| b |
| 128 |
| b |
| 128 |
设函数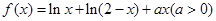 .
.
(Ⅰ) 当 时,求
时,求 的单调区间;
的单调区间;
(Ⅱ) 若 在
在 上的最大值为
上的最大值为 ,求
,求 的值.
的值.
【解析】第一问中利用函数 的定义域为(0,2),
的定义域为(0,2), .
.
当a=1时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
第二问中,利用当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
解:函数 的定义域为(0,2),
的定义域为(0,2), .
.
(1)当 时,
时, 所以
所以 的单调递增区间为(0,
的单调递增区间为(0, ),单调递减区间为(
),单调递减区间为( ,2);
,2);
(2)当 时,
时, >0, 即
>0, 即 在
在 上单调递增,故
上单调递增,故 在
在 上的最大值为f(1)=a 因此a=1/2.
上的最大值为f(1)=a 因此a=1/2.
古今中外,许多人致力于圆周率的研究与计算.为了计算出圆周率的越来越好的近似值,一代代的数学家为这个神秘的数贡献了无数的时间与心血.我国东汉的数学家刘徽利用“割圆术”计算圆的面积及圆周率π.“割圆术”被称为千古绝技,它的原理是用圆内接正多边形的面积去逼近圆的面积,具体计算如下:
在单位圆内作内接正六边形,其面积记为A1,边长记为a1,在此基础上作圆内接正12边形,面积记为A2,边长为a2…一直作下去,记该圆的内接正6×2n-1边形面积为An,边长为an.由于所考虑的是单位圆,计算出的An即为圆周率π的近似值,n越大,An与π越接近.
你能设计这样计算圆周率的一个算法吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com