
题目列表(包括答案和解析)
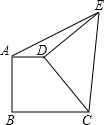 如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
如图直角梯形ABCD中,AD∥BC,AB⊥BC,∠BCD=45°,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )| A、1 | B、2 | C、3 | D、不能确定 |
 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连AE、CE,则△ADE的面积是( )| A、1 | B、2 | C、3 | D、不能确定 |
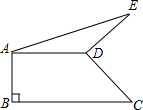 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=1,BC=3,以D为旋转中心,CD逆时针旋转90°得DE,则AE=
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=1,BC=3,以D为旋转中心,CD逆时针旋转90°得DE,则AE=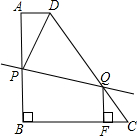 如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.
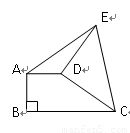
如图直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=8,CD=10.如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将梯形的腰CD以点D为中心逆时针旋转90°至DE,连接AE,CE,若△ADE的面积为3,那么BC的长为 ..
一.选择题:(本大题共15个题;每小题3分,共45分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
答案
B
C
A
C
D
A
B
A
D
B
A
B
D
A
A
 二.填空题:(本大题共5小题;每小题3分,共15分。)
二.填空题:(本大题共5小题;每小题3分,共15分。)
16.4 17. 36 ; 18. 20000; 19.
20.109
三.解答题:(本大题共6小题,共40分。解答应写出文字说明、证明过程或演算步骤。)
21.
解:(1)原式 ---1分
---1分
 ---2分
---2分
 ---3分
---3分
(2)
解:去分母得2x-5=3(2x-1)
即2x-5=6x-3---1分
∴4x=-2
x= ---2分
---2分
当x= 时,2x-1≠0
时,2x-1≠0
所以x= 是原方程的解---3分
是原方程的解---3分
22.(本题6分)
(1) C ---2分
(2)没有考虑 ---4分
---4分
(3) ---6分
---6分
23.(本题7分)
解(1)当x 30时,设函数关系式为y=kx+b
30时,设函数关系式为y=kx+b
则 -------2分
-------2分
解得
所以y=3x-30-------4分
(2)4月份上网20小时,应付上网费60元-------5分
(3) 由75=3x-30解得x=35,所以5月份上网35个小时. -------7分
24.(本题7分)
解:⑴设蓝球个数为 个
-------1分
个
-------1分
则由题意得 -------2分
-------2分

 答:蓝球有1个
--------3分
答:蓝球有1个
--------3分
--------4分
---------5分
∴ 两次摸到都是白球的概率 =
= ----------7分
----------7分
 25.(本题6分)
25.(本题6分)
证明:(1)∵AE=CF
∴AE+EF=CF+FE即AF=CE --------- 1分
又ABCD是平行四边形,∴AD=CB,AD∥BC
∴∠DAF=∠BCE ---------2分
在△ADF与△CBE中
 ---------3分
---------3分
∴△ADF≌△CBE(SAS)---------4分
(2)∵△ADF≌△CBE
∴∠DFA=∠BEC ---------5分
∴DF∥EB---------6分
26.(本题8分)
(1)由已知可得∠A,OE=60o , A,E=AE
由A′E// 轴,得△OA,E是直角三角形,
轴,得△OA,E是直角三角形,
设A,的坐标为(0,b)
AE=A,E= ,OE=2b
,OE=2b

所以b=1,A,、E的坐标分别是(0,1)与( ,1) --------3分
,1) --------3分
(2) 因为A,、E在抛物线上,所以

所以 ,函数关系式为
,函数关系式为
由 得
得
与x轴的两个交点坐标分别是( ,0)与(
,0)与( ,0)--------6分
,0)--------6分
(3) 不可能使△A′EF成为直角三角形。
∵∠FA,E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A,EF=90o或∠A,FE=90o
若∠A,EF=90o,利用对称性,则∠AEF=90o, A,、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A,FE=90o也不可能
所以不能使△A′EF成为直角三角形。--------8分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com