题目列表(包括答案和解析)
下列命题正确的是（ ）
A．单位向量都相等
B．若
与
是共线向量，与
是共线向量，则与是共线向量（ ）
C．
，则
D．若
与
是单位向量，则
A.a＞b
ac2＞bc2 B.
a＞b
C.
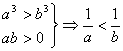D.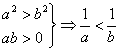
A.y=cosx的图象向右平移
得y=sinx的图象
B.y=sinx的图象向右平移
得y=cosx的图象
C.当φ＜0时，y=sinx向左平移φ个单位可得y=sin（x+φ）的图象
D.y=sin（2x+
）的图象由y=sin2x的图象向左平移
得到
A.所有的直角三角形都相似
B.所有的等腰三角形都相似
C.所有的等腰直角三角形都相似
D.所有的有一个角为30°的等腰三角形都相似
A．两个相等的向量，起点、方向、长度必要相同
B．若两个向量不共线，则这两个向量都是非零向量
C．两个有共同的起点的共线向量，其终点一定相同
D．两个共线的向量，其方向一定相同
CACD CCBA
9、
10、2:1 11、
12、
13、4
14、a<-1 15、
16、
17、解：（I）依题意
…………2分
…………4分
bn=8+8×(n-1)=8n …………5分
（II）
…………6分
…………12分
18、（1）3
（2）底面边长为2，高为4是，体积最大，最大体积为16
19、
略解、（1）因为f′(x)=3ax2+2x-1，依题意存在（2，+∞）的非空子区间使3ax2+2x-1>0成立，即
在x∈（2，+∞）某子区间上恒成立，令h(x)=
,求得h(x)的最小值为
，故
（2）由已知a>0
令f′(x)=3ax2+2x-1>0
得
故f(x)在区间（
）上是减函数，
即f(x)在区间（）上恒大于零。故当a>0时，函数在f(x)在区间（）上不存在零点
20、（1）f(1)=3………………………………………………………………………………（1分）
f(2)=6………………………………………………………………………………（2分）
当x=1时，y=2n，可取格点2n个；当x=2时,y=n，可取格点n个
∴f(n)=3n…………………………………………………………………………（4分）
（2）
………………………………………………（9分）
∴T1<T2=T3>T4>…>Tn
故Tn的最大值是T2=T3=
∴m≥………………………………………………………………（）
21、解：（Ⅰ）设
,
且
, …………………2分
…………………3分
.
………………………………………………4分
∴动点M的轨迹C是以O（0，0）为顶点，以（1，0）为焦点的抛物线（除去原点）.
…………………………………………5分
（Ⅱ）解法一：（1）当直线
垂直于
轴时，根据抛物线的对称性，有
；
……………6分
（2）当直线与轴不垂直时，依题意，可设直线的方程为
，
，则A，B两点的坐标满足方程组
消去并整理，得
,
. ……………7分
设直线AE和BE的斜率分别为
，则:
＝
. …………………9分
,
,
，
.
综合（1）、（2）可知.
…………………10分
解法二：依题意，设直线的方程为
，，则A，B两点的坐标满足方程组:
消去并整理，得
,
. ……………7分
设直线AE和BE的斜率分别为，则:
＝
. …………………9分
,
,
，
. ……………………………………………………10分
（Ⅲ）假设存在满足条件的直线
，其方程为
，AD的中点为
，与AD为直径的圆相交于点F、G，FG的中点为H，则
，点的坐标为
.
,
,
.
…………………………12分
,
令
，得
此时，
.
∴当
，即
时，
（定值）.
∴当时，满足条件的直线存在，其方程为
；当
时，满足条件的直线不存在.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com