
题目列表(包括答案和解析)
| π |
| 3 |
| π |
| 3 |
| 3 |
| 1 |
| 8 |
已知函数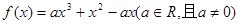 .如果存在实数
.如果存在实数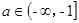 ,使函数
,使函数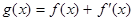 ,
,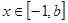
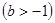 在
在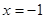 处取得最小值,则实数
处取得最小值,则实数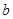 的最大值为 .
的最大值为 .
已知函数f(x)=a|x|+ (a>0,a≠1)
(a>0,a≠1)
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)= f( x),x∈[ 2,+∞), 满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
满足如下性质:若存在最大(小)值,则最大(小)值与a无关.试求a的取值范围.
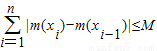 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: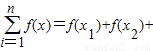 …+f(xn))
…+f(xn))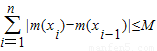 恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式:
恒成立,则称函数m(x)为在[p,q]上的有界变差函数,试判断函数f(x)是否为在[1,3]上的有界变差函数?若是,求M的最小值;若不是,请说明理由.(参考公式: …+f(xn))
…+f(xn))1. 2.
2. 3.{(1,-1)}
4.12 5.
3.{(1,-1)}
4.12 5. 
6. 7.
7. 8.直角
8.直角
9.解析:(1)(4).本题考查了独立性检验的基本思想及常用逻辑用语.由题意,得 ,
, ,所以,只有第一位同学的判断正确,即:有
,所以,只有第一位同学的判断正确,即:有 的把握认为“这种血清能起到预防感冒的作用”.由真值表知(1)(4)为真命题.
的把握认为“这种血清能起到预防感冒的作用”.由真值表知(1)(4)为真命题.
10.提示:设四棱锥的两组不相邻的侧面的交线分别为 m、n, 直线 m、n 确定了一个平面 β.作与 β 平行的平面 α, 与四棱锥的各个侧面相截,则截得的四边形必为平行四边形.而这样的平面 α 有无数多个.
11. 12.y=-x ±
12.y=-x ±
13.解:由 可化为xy =8+x+y
可化为xy =8+x+y
 x,y均为正实数,
x,y均为正实数, xy =8+x+y
xy =8+x+y (当且仅当x=y等号成立)
(当且仅当x=y等号成立)
即xy-2 -8
-8 可解得
可解得
 ,即xy
,即xy 16故xy的最小值为16.
16故xy的最小值为16.
14.
15.解:(1)A中2张钱币取1张,有2种情况,
B中3张钱币取1张,有3种情况,
∴互换一次有2´3 = 6种情况,
其中10元币恰是一张的情况有3种,
∴A袋中10元钱币恰是一张的概率为P1 = .答略
.答略
(2)A袋中恰有一张10元币的概率为P1 =  ;
;
A袋中恰有两张10元币的概率为P2 =  ;
;
∴ A袋中10元钱币至少是一张的概率P = P1 + P2
=  +
+
 =
=  .
.
另解:. A袋中恰有0张10元币的概率为P0
=  ,
,
∴A袋中10元钱币至少是一张的概率P = 1 ? P0 =  .答略.
.答略.
16.解: (1)证明:取PB中点Q,连结MQ、NQ,因为M、N分别是棱AD、PC中点,所以
(1)证明:取PB中点Q,连结MQ、NQ,因为M、N分别是棱AD、PC中点,所以
QN//BC//MD,且QN=MD,于是DN//MQ.
 .
.
(2)
又因为底面ABCD是 、边长为
、边长为 的菱形,且M为AD中点,
的菱形,且M为AD中点,
所以 .
.
又
所以 .
.

(3)因为M是AD中点,所以点A与D到平面PMB等距离.
过点D作 于H,由(2)平面PMB
于H,由(2)平面PMB 平面PAD,所以
平面PAD,所以 .
.
故DH是点D到平面PMB的距离.

所以点A到平面PMB的距离为 .
.
17.解:(1)设 中角
中角 的对边分别为
的对边分别为 ,则由
,则由 ,
,
可得 ,所以
,所以
(2)


因为 ,
, ,所以
,所以
即当 时,
时, ;当
;当 时,
时,
18.解:(1)直线l1: x+my-m-2=0与l2: mx-y OB,所以A,M,B,O四点共圆,且AB即圆的直径,又A(m+2,0),B (0,1
OB,所以A,M,B,O四点共圆,且AB即圆的直径,又A(m+2,0),B (0,1

整理得:
(2)当AB与OM垂直于点P时,由垂径定理得点P为OM中点(1, ),不妨取OA中点Q(
),不妨取OA中点Q( ,0),又m
,0),又m ,否则AM垂直x轴,四边形AMBO为矩形,AB与OM不垂直,所以
,否则AM垂直x轴,四边形AMBO为矩形,AB与OM不垂直,所以 ,
, ,
,
 ,
, 得证.
得证.
19.解:(1)当n为奇数时,有2n+1=(2+1)(2n-1-2n-2+…-2+1)=3(2n-1-2n-2+…-2+1)
所以2n+1是最小的数;又2n+1-1=(2n+1+2)-3=2(2n+1)-3,所以2n+1-1是最大的数.
(2)由(1)知当n为奇数时,An中的各个元素组成以2n+1为首项,3为公差的等差数列,设项数为m,则2n+1-1=2n+1+3(m-1),所以m= ,所以当n是奇数时,An中的所有元素之和为
,所以当n是奇数时,An中的所有元素之和为 ;
;
当n为偶数时,n-1时奇数,由(1)可知2n-1+1是3的倍数,因此2n+2=2(2n-1+1)是3的倍数;同理,2n+1-2=2(2n-1)是3的倍数.所以当n为偶数时,An中的各个元素组成以2n+2为首项,3为公差的等差数列,设项数为m,则2n+1-2=2n+2+3(m-1),所以m= ,所以当n是偶数时,An中的所有元素之和为
,所以当n是偶数时,An中的所有元素之和为 .
.
20.解:(1) ,∴可设
,∴可设 ,
,
因而 ①
①

 =
= ,
,
∵ 在区间
在区间 内单调递减,
内单调递减,
∴ 在
在 上的函数值非正,
上的函数值非正,
由于 ,对称轴
,对称轴 ,故只需
,故只需 ,注意到
,注意到 ,∴
,∴ ,得
,得 或
或 (舍去).
(舍去).
故所求 的取值范围是
的取值范围是 .
.
(2) 时,方程
时,方程 仅有一个实数根,即证方程
仅有一个实数根,即证方程 仅有一个实数根.令
仅有一个实数根.令
 ,由
,由 ,得
,得 ,
, ,易知
,易知 在
在 ,
, 上递增,在
上递增,在 上递减,
上递减, 的极大值
的极大值 ,故函数
,故函数 的图像与
的图像与 轴仅有一个交点,∴
轴仅有一个交点,∴ 时,方程
时,方程 仅有一个实数根,得证.
仅有一个实数根,得证.
(3)设  =
=  x2+x+1,
x2+x+1, =1,对称轴为
=1,对称轴为 ,.
,.
由题意,得 或
或
解出 ,故使|
,故使| |≤3成立的充要条件是
|≤3成立的充要条件是
附加题:
1.证明:如图,分别过点E、F作AB的垂线,G、H为垂足,连FA、EB.易知
DB2=FB2=AB?HB,
AD2=AE2=AG?AB.
 二式相减,得
二式相减,得
DB2-AD2=AB?(HB-AG),
或 (DB-AD)?AB=AB?(HB-AG).
于是,DB-AD=HB-AG,
或 DB-HB=AD-AG.
就是DH=GD.
显然,EG∥CD∥FH.
故CD平分EF.2.
2.解:由上题可知 1 =
1 = ,
, 2
=
2
= 是矩阵M=
是矩阵M= 分别对应特征值
分别对应特征值 1=1,
1=1, 2=4的两个特征向量,而
2=4的两个特征向量,而 1与
1与 2不共线.又
2不共线.又 =
= =3
=3 +(-2)
+(-2)
∴M20 =
M20(3
=
M20(3 2+(-2)
2+(-2) 1)=
1)= 2+(-2) M20
2+(-2) M20 1
1
=3 220
220 2+(-2)×
2+(-2)× 120
120 1=3×420×
1=3×420× +(-2)×120×
+(-2)×120×
= ≈
≈
答:20个时段后这两个种群的数量都趋向于3×420.
3.证明:以F为极点,极轴与x轴正向重合建立极坐标系.
设抛物线方程 ,A(ρ1,θ),B(ρ2,θ+π),
,A(ρ1,θ),B(ρ2,θ+π),
则AB=ρ1+ρ2= = 4p,sin2θ= ,θ=
,θ=
4.(Ⅰ)证明:(?)当 时,原不等式成立;当
时,原不等式成立;当 时,左边
时,左边 ,右边
,右边 ,因为
,因为 ,所以左边
,所以左边 右边,原不等式成立;
右边,原不等式成立;
(?)假设当 时,不等式成立,即
时,不等式成立,即 ,则当
,则当 时,
时,
 ,
, ,于是在不等式
,于是在不等式 两边同乘以
两边同乘以 得
得
 ,
,
所以 .即当
.即当 时,不等式也成立.
时,不等式也成立.
综合(?)(?)知,对一切正整数 ,不等式都成立.
,不等式都成立.
5.(1)设事件 为A,则在7次抛骰子中出现5次奇数,2次偶数
为A,则在7次抛骰子中出现5次奇数,2次偶数
而抛骰子出现的奇数和偶数的概率为p是相等的,且为
根据独立重复试验概率公式:
(2)若
即前2次抛骰子中都是奇数或都是偶数.
若前2次都是奇数,则必须在后5次中抛出3次奇数2次偶数,
其概率:
若前2次都是偶数,则必须在后5次中抛出5次奇数,其概率:

 所求事件的概率
所求事件的概率
6.以下解答仅供参考,按学生实际解答给分.
解:(1) 条直线将一个平面最多分成
条直线将一个平面最多分成 个部分(
个部分( ),与(2)合并证明;
),与(2)合并证明;
(2) 个平面最多将空间分割成
个平面最多将空间分割成 个部分(
个部分( ).
).
证明:设 个
个 维空间可将
维空间可将 维空间最多分成
维空间最多分成 个部分,则只需证明
个部分,则只需证明

 ,这里
,这里 ∈
∈
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com