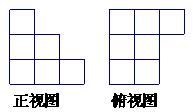10、用单位立方块搭一个几何体，使它的正视图和俯视图如图所示，则它的体积的最小值与最大值分别为（　　）

A、7，10

B、7，12

C、10，12

D、10，16

查看答案和解析>>

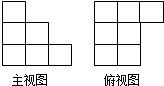11、用单位立方块搭一个几何体，使它的主视图和俯视图如右图所示，则它的体积的最小值为

10

，最大值分别为

16

查看答案和解析>>

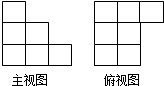8、用单位立方块搭一个几何体，使它的主视图和俯视图如右图所示，则它的体积的最小值与最大值分别为（　　）

A、9与13

B、7与10

C、10与16

D、10与15

查看答案和解析>>

查看答案和解析>>

用单位立方块搭一个几何体，使它的主视图和俯视图如图所示，则它的体积的最小值与最大值分别为（　　）

A．9与13

B．7与10

C．10与16

D．10与15

查看答案和解析>>

一、填空题：本大题共14小题，每小题5分，共70分．

1．　2．2i　3．（）或（）　4．16　　5．a≥-8     6．64       7．（1）(3)(4)  8．6    9． 　 10．  11．1　     12．   13．(－∞，1)

14．，提示：设，则，故为增函数，由a＜b，有，也可以考虑特例，如f(x)=x²

二、解答题：解答应写出文字说明，证明过程或演算步骤．

15．（1）                     

                                          5分

即

为等腰三角形.                                             8分

（2）由（I）知

                        12分

                                                           14分

16．（1）由图形可知该四棱锥和底面ABCD是菱形，且有一角为，边长为2，

锥体高度为1。

设AC，BD和交点为O，连OE，OE为△DPB的中位线，

OE//PB，                                             3分

EO面EAC，PB面EAC内，PB//面AEC。          6分

（2）过O作OFPA垂足为F , 

在Rt△POA中，PO=1，AO=，PA=2，在Rt△POB中，PO=1，BO=1，PB=，   8分

过B作PA的垂线BF，垂足为F，连DF，由于△PAB≌△PAD，故DF⊥PA，DF∩BF=F，因此PA⊥面BDF.                                                  10分

在等腰三角形PAB中解得AF=,进而得PF=               

即当时，PA面BDF，                       12分

此时F到平面BDC的距离FH=

            14分

17．(1)                     4分

椭圆方程为                                7分

（2）         10分

＝2       14分

所以P在DB延长线与椭圆交点处，Q在PA延长线与圆的交点处，得到最大值为．  15分

18．（1）DM=，DN=，MF=，EN=，                          4分

=EF=DM+DN-MF-EN=+－－

=       （）                                        7分

（2）“平板车要想顺利通过直角走廊”即对任意角（），平板车的长度不能超过，即平板车的长度；记 ，有=，

===，                                            10分

此后研究函数的最小值，方法很多；如换元（记，则）或直接求导，以确定函数在上的单调性；当时取得最小值。                    15分

19． (1)点(n，)在直线y＝x＋上，∴＝n＋，即S_n＝n²＋n，

a_n＝n＋5．                                                                     3分

∵b_n+2－2b_n+1＋b_n＝0(nÎN^*)，∴b_n+2－b_n+1＝ b_n+1－b_n＝…＝ b₂－b₁．

∴数列{b_n}是等差数列，∵b₃＝11，它的前9项和为153，设公差为d，

则b₁＋2d＝11，9b₁＋×d＝153，解得b₁＝5，d＝3．∴b_n＝3n＋2．                  6分

(2)由(1)得，c_n＝ ＝ ＝(－)，

∴T_n＝b₁＋b₂＋b₃＋…＋b_n＝(1－)＋(－)＋(－)＋…＋(－)

＝(1－)．                                                           9分

∵T_n＝(1－)在nÎN^*上是单调递增的，∴T_n的最小值为T₁＝．

∵不等式T_n＞对一切nÎN^*都成立，∴＜．∴k＜19．∴最大正整数k的值为18．11分

(3) nÎN^*，f(n)＝＝

当m为奇数时，m＋15为偶数；当m为偶数时，m＋15为奇数．

若f(m＋15)＝5f(m)成立，则有3（m＋15）＋2＝5(m＋5)(m为奇数)

或m＋15＋5＝5（3m＋2）(m为偶数)．                                      13分

解得m＝11．所以当m＝11时，f(m＋15)＝5f(m)．                             16分

20．（1）．                                       2分

  　当时，，在上单调递增；                     3分

 　 当时，时，，在上单调递减；         

时，，在上单调递增．                 5分

综上所述，当时，的单调递增区间为；当时，的单调递增区间为，单调递减区间为．                                         6分

（2）充分性：a=1时，由（1）知，在x=1处有极小值也是最小值，

即。而在上单调递减，在上单调递增，

在上由唯一的一个零点x=1．                               9分

必要性：=0在上有唯一解，且a>0, 由（1）知，在x=a处有极小值也是最小值f(a)，f(a)=0,即．

令，．

当时，，在上单调递增；当a>1时，，

在上单调递减。，=0只有唯一解a=1．

=0在上有唯一解时必有a=1．                           12分

综上：在a>0时，=0在上有唯一解的充要条件是a=1．

（3）证明：∵1<x<2,∴.

 令，∴，14分

由（1）知，当a=1时，，∴，∴．

∴，∴F（x）在（1，2）上单调递增，∴，

∴。∴．             16分

附加题答案

1．解：如图，连结OC，因,因此,由于,

所以，又得;      5分   

又因为,得,那么,

从而，于是。            10分   

2．解：设A=，由题知=，=3 

即，                      5分

 ∴         ∴A=       10分

3．解： 直线的参数方程为 为参数）故直线的普通方程为  3分

   因为为椭圆上任意点，故可设其中.

  因此点到直线的距离是            7分

所以当，时，取得最大值.                              10分 

4. 证（1）　

∵，，

∴| f(x₁)－f(x₂)|＜| x₁－x₂|                       5分   

（2），∴f(a)＋f(b) ≤

∵    ，

∴                     10分

 5.解：（1）为实数，即为实数，  ∴b＝3            2分

又依题意，b可取1，2，3，4，5，6

故出现b＝3的概率为

即事件“为实数”的概率为                                            5分

（2）由已知，                           6分

可知，b的值只能取1、2、3                          

当b＝1时， ，即a可取1，2，3

当b＝2时， ，即a可取1，2，3

当b＝3时， ，即a可取2                

由上可知，共有7种情况下可使事件“”成立                           9分

又a，b的取值情况共有36种

故事件“”的概率为                                           10分

6.解：（1）∵A₁B₁C₁－ABC为直三棱柱  ∴CC₁⊥底面ABC  ∴CC₁⊥BC

       ∵AC⊥CB   ∴BC⊥平面A₁C₁CA

∴A₁B与平面A₁C₁CA所成角的正切值               3分

（2）分别延长AC，A₁D交于G. 过C作CM⊥A₁G 于M，连结BM

∵BC⊥平面ACC­₁A₁   ∴CM为BM在平面A₁C₁CA的内射影

∴BM⊥A₁G    ∴∠CMB为二面角B―A₁D―A的平面角

    平面A₁C₁CA中，C₁C=CA=2，D为C₁C的中点

∴CG=2，DC=1 在直角三角形CDG中，  

   , 

即二面角B―A₁D―A的平面角的正切值为     6分

（3）在线段AC上存在一点F，使得EF⊥平面A₁BD .

其位置为AC中点，证明如下：

∵A₁B₁C₁―ABC为直三棱柱 ， ∴B₁C₁//BC

∵由（1）BC⊥平面A₁C₁CA，∴B₁C₁⊥平面A₁C₁CA

∵EF在平面A₁C₁CA内的射影为C₁F ，F为AC中点 ∴C₁F⊥A₁D  ∴EF⊥A₁D

同理可证EF⊥BD,         ∴EF⊥平面A₁BD

∵E为定点，平面A₁BD为定平面,点F唯一            10分

解法二：（1）同解法一                               3分

（2）∵A₁B₁C₁―ABC为直三棱住   C₁C=CB=CA=2 , AC⊥CB  D、E分别为C₁C、B₁C₁的中点, 建立如图所示的坐标系得

C（0，0，0） B（2，0，0）  A（0，2，0）

C₁（0，0，2）  B₁（2，0，2）  A­₁（0，2，2）

D（0，0，1）  E（1，0，2）

  设平面A₁BD的法向量为

平面ACC₁A₁­的法向量为=（1，0，0） 

即二面角B―A₁D―A的平面角的正切值为               6分

（3）在线段AC上存在一点F，设F（0，y，0）使得EF⊥平面A₁BD

欲使EF⊥平面A₁BD    由（2）知，当且仅当//

∴存在唯一一点F（0，1，0）满足条件. 即点F为AC中点        10分