假设关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料：

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

若由资料知，y对x呈线性相关关系.试求：

(1)线性回归方程；

(2)估计使用年限为10年时，维修费用约是多少？思路分析：本题考查线性回归方程的求法和利用线性回归方程求两变量间的关系.

解：(1)

i	1	2	3	4	5
xi	2	3	4	5	6
yi	2.2	3.8	5.5	6.5	7.0
xiyi	4.4	11.4	22.0	32.5	42.0

b==1.23,

a=-b=5-1.23×4=0.08.

所以，回归直线方程为=1.23x+0.08.

(2)当x=10时，=1.23×10+0.08=12.38(万元),

即估计使用10年时维修费约为12.38万元.

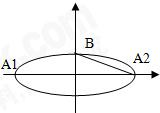已知椭圆

x2

a2

+

y2

b2

=1(a＞b＞0)，A₁、A₂、B是椭圆的顶点（如图），直线l与椭圆交于异于椭圆顶点的P、Q两点，且l∥A₂B．若此椭圆的离心率为

3

2

，且|A2B|=

5

（Ⅰ）求此椭圆的方程；
（Ⅱ）设直线A₁P和直线BQ的倾斜角分别为α、β，试判断α+β是否为定值？若是，求出此定值；若不是，请说明理由．

我国是水资源比较贫乏的国家之一，各地采用价格调控等手段以达到节约用水的目的．
某市用水收费标准是：水费=基本费+超额费+定额损耗费，且有如下三条规定：
①若每月用水量不超过最低限量m立方米时，只付基本费9元和每户每月定额损耗费a元；
②若每月用水量超过m立方米时，除了付基本费和定额损耗费外，超过部分每立方米付n元的超额费；
③每户每月的定额损耗费a不超过5元．
（1）求每户每月水费y（元）与月用水量x（立方米）的函数关系；
（2）该市一家庭今年第一季度每月的用水量和支付的费用如下表所示：

月份	用水量（立方米）	水费（元）
一	4	17
二	5	23
三	2.5	11

试分析该家庭今年一、二、三各月份的用水量是否超过最低限量，并求m，n，a的值．

A、1

B、1或4

C、1或5

D、4或5