椭圆+ =1的右焦点为F,过点A(1,3),点M在椭圆上,当|AM|+2|MF|为最小值时,求点M的坐标.

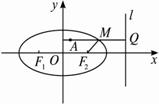
思路分析:关键是对于|AM|+2|MF|中的“2”的处理,把2|MF|转化为M到右准线的距离,从而得到最小值.一般地,求|AM|+|MF|均可用此法.?

一个等比数列的首项为1,项数是偶数,其奇数项的和为85,偶数项的和为170,求此数列的公比和项数.

思路分析:因奇数项和与偶数项和不同,项数相同,可知其公比q≠1,故可直接套用求和公式,列方程组解决.

已知关于x的方程(1-a)x²+(a+2)x-4=0,a∈R,求:?

(1)方程有两个正根的充要条件；

(2)方程至少有一个正根的充要条件.?

思路分析:先求出方程有两个实根的充要条件,再讨论x²的系数及运用根与系数的关系分别求出要求的充要条件.

求经过点P(1,2)的直线,且使A(2,3),B(0, -5)到它的距离相等的直线方程.

参考答案与解析:思路分析：由题目可获取以下主要信息:

①所求直线过点P(1,2);

②点A(2,3),B(0,-5)到所求直线距离相等.

假设关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料：

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

若由资料知，y对x呈线性相关关系.试求：

(1)线性回归方程；

(2)估计使用年限为10年时，维修费用约是多少？思路分析：本题考查线性回归方程的求法和利用线性回归方程求两变量间的关系.

解：(1)

i	1	2	3	4	5
xi	2	3	4	5	6
yi	2.2	3.8	5.5	6.5	7.0
xiyi	4.4	11.4	22.0	32.5	42.0

b==1.23,

a=-b=5-1.23×4=0.08.

所以，回归直线方程为=1.23x+0.08.

(2)当x=10时，=1.23×10+0.08=12.38(万元),

即估计使用10年时维修费约为12.38万元.