
题目列表(包括答案和解析)
已知数列 的前
的前 项和为
项和为 ,且
,且 (
( N*),其中
N*),其中 .
.
(Ⅰ) 求 的通项公式;
的通项公式;
(Ⅱ) 设 (
( N*).
N*).
①证明:  ;
;
② 求证: .
.
【解析】本试题主要考查了数列的通项公式的求解和运用。运用 关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到
关系式,表示通项公式,然后得到第一问,第二问中利用放缩法得到 ,②由于
,②由于 ,
,
所以 利用放缩法,从此得到结论。
利用放缩法,从此得到结论。
解:(Ⅰ)当 时,由
时,由 得
得 . ……2分
. ……2分
若存在 由
由 得
得 ,
,
从而有 ,与
,与 矛盾,所以
矛盾,所以 .
.
从而由 得
得 得
得 . ……6分
. ……6分
(Ⅱ)①证明:
证法一:∵ ∴
∴
∴
∴ .…………10分
.…………10分
证法二: ,下同证法一.
……10分
,下同证法一.
……10分
证法三:(利用对偶式)设 ,
, ,
,
则 .又
.又 ,也即
,也即 ,所以
,所以 ,也即
,也即 ,又因为
,又因为 ,所以
,所以 .即
.即
 ………10分
………10分
证法四:(数学归纳法)①当 时,
时,  ,命题成立;
,命题成立;
②假设 时,命题成立,即
时,命题成立,即 ,
,
则当 时,
时,

 即
即
即
故当 时,命题成立.
时,命题成立.
综上可知,对一切非零自然数 ,不等式②成立. ………………10分
,不等式②成立. ………………10分
②由于 ,
,
所以 ,
,
从而 .
.
也即
已知递增等差数列 满足:
满足: ,且
,且 成等比数列.
成等比数列.
(1)求数列 的通项公式
的通项公式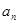 ;
;
(2)若不等式 对任意
对任意 恒成立,试猜想出实数
恒成立,试猜想出实数 的最小值,并证明.
的最小值,并证明.
【解析】本试题主要考查了数列的通项公式的运用以及数列求和的运用。第一问中,利用设数列 公差为
公差为 ,
,
由题意可知 ,即
,即 ,解得d,得到通项公式,第二问中,不等式等价于
,解得d,得到通项公式,第二问中,不等式等价于 ,利用当
,利用当 时,
时, ;当
;当 时,
时, ;而
;而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 然后加以证明即可。
然后加以证明即可。
解:(1)设数列 公差为
公差为 ,由题意可知
,由题意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等价于 ,
,
当 时,
时, ;当
;当 时,
时, ;
;
而 ,所以猜想,
,所以猜想, 的最小值为
的最小值为 . …………8分
. …………8分
下证不等式 对任意
对任意 恒成立.
恒成立.
方法一:数学归纳法.
当 时,
时, ,成立.
,成立.
假设当 时,不等式
时,不等式 成立,
成立,
当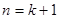 时,
时, ,
…………10分
,
…………10分
只要证  ,只要证
,只要证  ,
,
只要证  ,只要证
,只要证  ,
,
只要证  ,显然成立.所以,对任意
,显然成立.所以,对任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:单调性证明.
要证 
只要证  ,
,
设数列 的通项公式
的通项公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以对 ,都有
,都有 ,可知数列
,可知数列 为单调递减数列.
为单调递减数列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值为
的最小值为 .
.
中国篮球职业联赛某赛季的总决赛在某两队之间角逐,采用七局四胜制,即若有一队先胜四场,则此队获胜,比赛就此结束.因两队实力相当,每场比赛获胜的可能性相等.据以往资料统计,第一场比赛组织者可获门票收入30万元,以后每场比赛门票收入都比上一场增加10万元,当两队决出胜负后.问:
(1)组织者在此次决赛中要获得门票收入为180万元须比赛多少场?
(2)组织者在此次决赛中获得门票收入不少于330万元的概率为多少?
分析:本题是一个概率与数列的综合试题,可以首先求出收入的通项公式,从而得出比赛的场数,再确定其概率.
2007年12月29日第十届全国人大常委会第三十一次会议表决通过了《关于修改〈中华人民共和国个人所得税法〉的决定》,将个人所得税工资、薪金所得减除费用标准由每月1600元提高到每月2000元,同时明确自2008年3月1日起施行.即公民全月工资,薪金所得不超过2000元的部分不必纳税,超过2000元的部分应纳税,此项税款按下表分段累进计算:

注明:上表中“全月应纳税所得额”是从月工资、薪金收入中减去2000元后的余额.例如某人月工资、薪金收入为3000元,减去2000元,应纳税所得额为1000元,由税率表知其中500元税率为5%,另外500元的税率为10%,所以此人应纳个人所得税为500×5%+500×10%=75元.
(1)请写出月工资,薪金的个人所得税y关于工资,薪金收入x(0<x≤5000)的函数表达式;
(2)某高中数学教师在2008年10月份缴纳的个人所得税是40元,试求他这个月的工资,薪金收入是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com