
题目列表(包括答案和解析)
设集合P={1,2,3,4,5},对任意k∈P和正整数m,记f(m,k)= ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
设集合 ,
,
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)当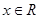 时,没有元素
时,没有元素 使得
使得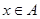 与
与 同时成立,求实数
同时成立,求实数 的取值范围。
的取值范围。
 ,且B∩C≠
,且B∩C≠ ,求实数m的取值范围;
,求实数m的取值范围; 成立,若存在,求实数的取值范围;若不存在,请说明理由。
成立,若存在,求实数的取值范围;若不存在,请说明理由。 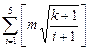 ,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。
,其中[a]表示不大于a的最大整数。求证:对任意正整数n,存在k∈P和正整数m,使得f(m,k)=n。 集合
集合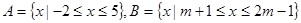 ,
,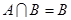 ,求实数
,求实数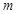 的取值范围;
的取值范围;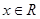 时,没有元素
时,没有元素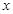 使得
使得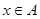 与
与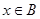 同时成立,求实数
同时成立,求实数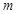 的取值范围。
的取值范围。
一、选择题
1.D 2.A 3.C 4.B 5.D 6.A 7.A 8.A 9.B 10.D
|