
题目列表(包括答案和解析)
 (2008?北京)(1)用示波器观察某交流信号时,在显示屏上显示出一个完整的波形,如图.经下列四组操作之一,使该信号显示出两个完整的波形,且波形幅度增大.此组操作是
(2008?北京)(1)用示波器观察某交流信号时,在显示屏上显示出一个完整的波形,如图.经下列四组操作之一,使该信号显示出两个完整的波形,且波形幅度增大.此组操作是| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |
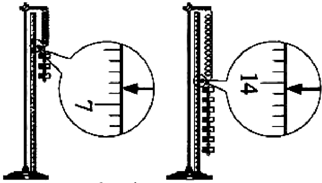
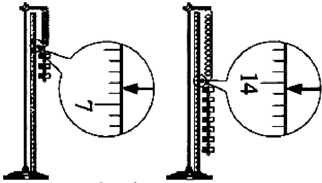 ②实验中,L3和L2两个值还没有测定,请你根据上图将这两个测量值填入记录表中.
②实验中,L3和L2两个值还没有测定,请你根据上图将这两个测量值填入记录表中.| (d1+d2+d3+d4) |
| 4×4 |
| (d1+d2+d3+d4) |
| 4×4 |
如图所示,1、2两细绳与水平车顶的夹角分 别为300和600,物体质量为m,现让小车以2g(g为重力加速度)的加速度向右做匀加速直线运动,当物体与车保持相对静止时,求:绳1中弹力的大小?
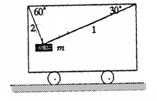
下面是一位同学的解法
解:以物体m为研究对象,受力分析如图,由牛顿第二定律得:
x:T1cos300-T2cos600=ma
y:T1sin300 +T2sin600=mg
解得: T1=(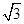 +
+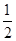 )mg
)mg
你认为该同学的解法正确吗?如有错误请写出正确的解法。

A.调整X增益旋钮和竖直位移旋钮
B.调整X增益旋钮和扫描微调旋钮
C.调整扫描微调旋钮和Y增益旋钮
D.调整水平位移旋钮和Y增益旋钮
(2)某同学和你一起探究弹力和弹簧伸长的关系,并测弹簧的劲度系数k。做法是先将待测弹簧的一端固定在铁架台上,然后将最小刻度是毫米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的指针恰好落在刻度尺上。当弹簧自然下垂时,指针指示的刻度数值记作L0;弹簧下端挂一个
①下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它们的代表符号分别是 和 .
测量记录表:
代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
刻度数值/cm | 1.70 | 3.40 | 5.10 |
| 8.60 | 10.3 | 12.1 |
|

②实验中,L3和L7两个值还没有测定,请你根据上图将这两个测量值填入记录表中。
③为充分利用测量数据,该同学将所测得的数值按如下方法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90cm,d2=L5-L1=6.90cm,d3=L6-L2=7.00cm。
请你给出第四个差值:d4= = cm。
④根据以上差值,可以求出每增加![]() 。
。![]() 用d1、d2、d3、d4
用d1、d2、d3、d4
表示的式子为:![]() = ,
= ,
代入数据解得![]() = cm。
= cm。
⑤计算弹簧的劲度系数k= N/m。(g取
(14分)
(1)开普勒行星运动第三定律指出:行星绕太阳运动的椭圆轨道的半长轴a的三次方与它的公转周期T的二次方成正比,即![]() ,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
,k是一个对所有行星都相同的常量。将行星绕太阳的运动按圆周运动处理,请你推导出太阳系中该常量k的表达式。已知引力常量为G,太阳的质量为M太。
(2)开普勒定律不仅适用于太阳系,它对一切具有中心天体的引力系统(如地月系统)都成立。经测定月地距离为3.84×108m,月球绕地球运动的周期为2.36×106S,试计算地球的质M地。(G=6.67×10-11Nm2/kg2,结果保留一位有效数字)
【解析】:(1)因行星绕太阳作匀速圆周运动,于是轨道的半长轴a即为轨道半径r。根据万有引力定律和牛顿第二定律有
![]() ①
①
于是有 ![]() ②
②
即 ![]() ③
③
(2)在月地系统中,设月球绕地球运动的轨道半径为R,周期为T,由②式可得
![]() ④
④
解得 M地=6×1024kg ⑤
(M地=5×1024kg也算对)
23.【题文】(16分)
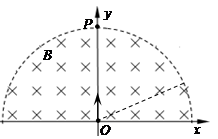 如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
如图所示,在以坐标原点O为圆心、半径为R的半圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B,磁场方向垂直于xOy平面向里。一带正电的粒子(不计重力)从O点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从P点射出。
(1)求电场强度的大小和方向。
(2)若仅撤去磁场,带电粒子仍从O点以相同的速度射入,经![]() 时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场,带电粒子仍从O点射入,且速度为原来的4倍,求粒子在磁场中运动的时间。
| 代表符号 | L0 | L1 | L2 | L3 | L4 | L5 | L6 | L7 |
| 刻度数值/cm | 1.70 | 3.40 | 5.10 | 8.60 | 10.3 | 12.1 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com