
题目列表(包括答案和解析)
..如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(1)设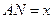 (单位:米),要使花
(单位:米),要使花 坛AMPN的面积大于32平方米,求
坛AMPN的面积大于32平方米,求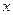 的取值范围;
的取值范围;
|
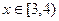 (单位:米),则当AM,A
(单位:米),则当AM,A N的长度分别是多少
N的长度分别是多少 时,花坛AMPN的面积最大?并求出最大面积。
时,花坛AMPN的面积最大?并求出最大面积。 ..(本小题满分12分)
已知: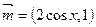 ,
,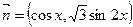 ,
,
函数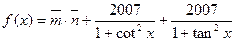 .
.
(1)化简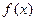 的解析式,并求函数的单调递减区间;
的解析式,并求函数的单调递减区间;
(2)在△ABC中,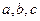 分别是角A,B,C的对边,已知
分别是角A,B,C的对边,已知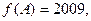
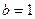 ,△ABC的面积为
,△ABC的面积为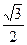 ,求
,求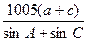 的值.
的值.
..在 中,
中, 分别为内角
分别为内角 所对的边,且
所对的边,且 .
.
现给出三个条件:① ; ②
; ②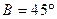 ;③
;③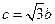 .试从中选出两个可以确定
.试从中选出两个可以确定 的条件,并以此为依据求
的条件,并以此为依据求 的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的
的面积.(只需写出一个选定方案即可)你选择的条件是 (用序号填写);由此得到的 的面积为
的面积为
..(满分8分)已知数列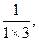
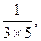
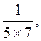
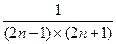 ,
,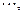
(1)计算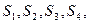
(2)根据(1)的计算结果,猜想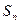 的表达式
的表达式 ,并用数学归纳法进行证明。
,并用数学归纳法进行证明。
..(本小题满分12分)
数列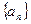 的各项均为正数,
的各项均为正数,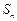 为其前
为其前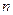 项和,对于任意
项和,对于任意 ,总有
,总有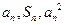 成等差数列.
成等差数列.
(1)求数列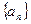 的通项公式;
的通项公式;
(2)设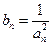 ,数列
,数列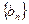 的前
的前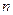 项和为
项和为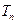 ,求证:
,求证: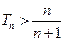 .
.
一、选择题:
1、A 2、B 3、A 4、D 5、D 6、C7、A 8、C9、A10、C 11、A 12、B
二、填空题:
13、 {1,2,3} 14、 充分而不必要条件 15、 2 16、.files/image040.gif) 17、 48
17、 48
18、 4 19、.files/image279.gif) 20、
20、.files/image281.gif) 21、4 22、
21、4 22、.files/image283.gif)
23、.files/image285.gif) 24、
24、.files/image287.gif) 25、
25、.files/image289.gif) 26、①②
26、①②
三、解答题:
27解:由题设,当.files/image291.gif) 时,
时,.files/image293.gif)
.files/image295.gif)
由题设条件可得.files/image297.gif)
.files/image299.gif)
(2)由(1)当.files/image301.gif)
这时数列.files/image303.gif) =
=.files/image305.gif)
.files/image307.gif)
这时数列.files/image309.gif) ①
①
上式两边同乘以.files/image311.gif) ,得
,得
.files/image313.gif) ②
②
①―②得
.files/image315.gif)
=.files/image317.gif)
所以.files/image319.gif)
28解:(1)因BC∥B
且B.files/image321.gif) 平面MNB1, BC
平面MNB1, BC.files/image323.gif) 平面MNB1,
平面MNB1,
故BC∥平面MNB1.
(2)因BC⊥AC,且ABC-A1B
故BC⊥平面ACC
因BC.files/image321.gif) 平面A1CB,
平面A1CB,
故平面A1CB⊥平面ACC
29解:设.files/image325.gif) 延长
延长.files/image327.gif) 交
交.files/image329.gif) 于
于.files/image097.gif)
.files/image332.gif)
.files/image334.gif)
.files/image336.gif)
.files/image338.gif)
.files/image340.gif)
.files/image230.gif)
.files/image342.gif)
令.files/image344.gif)
.files/image346.gif) -10
-10
故当.files/image348.gif) 时,S的最小值为
时,S的最小值为.files/image350.gif) ,当
,当.files/image352.gif) 时 S 的
时 S 的.files/image354.gif)
30解:.files/image356.gif)
点.files/image358.gif)
∴圆心.files/image360.gif)
(2)由直线.files/image362.gif)
∴设.files/image364.gif)
将直线.files/image366.gif) 代人圆方程
代人圆方程
得.files/image368.gif)
.files/image370.gif)
得.files/image372.gif)
由韦达定理得.files/image374.gif)
.files/image376.gif)
又.files/image378.gif) ∴
∴.files/image380.gif)
即.files/image382.gif)
解得.files/image384.gif)
∴所求直线方程为.files/image386.gif)
31解:(1)当a=1时,.files/image388.gif) ,其定义域是
,其定义域是.files/image390.gif) ,
,
.files/image392.gif)
令.files/image394.gif) ,即
,即.files/image396.gif) ,解得
,解得.files/image398.gif) 或
或.files/image400.gif) .
.
.files/image402.gif) ,
,.files/image404.gif) 舍去.
舍去.
当.files/image406.gif) 时,
时,.files/image408.gif) ;当
;当.files/image137.gif) 时,
时,.files/image411.gif) .
.
∴函数.files/image033.gif) 在区间(0,1)上单调递增,在区间(1,+∞)上单调递减
在区间(0,1)上单调递增,在区间(1,+∞)上单调递减
∴当x=1时,函数.files/image033.gif) 取得最大值,其值为
取得最大值,其值为.files/image414.gif) .
.
当.files/image416.gif) 时,
时,.files/image418.gif) ,即
,即.files/image420.gif) .
.
∴函数.files/image033.gif) 只有一个零点.
只有一个零点.
(2)法一:因为.files/image422.gif) 其定义域为
其定义域为.files/image390.gif) ,
,
所以.files/image425.gif)
①当a=0时,.files/image427.gif) 在区间
在区间.files/image390.gif) 上为增函数,不合题意
上为增函数,不合题意
②当a>0时,.files/image430.gif) 等价于
等价于.files/image432.gif) ,即
,即.files/image434.gif) .
.
此时.files/image033.gif) 的单调递减区间为
的单调递减区间为.files/image437.gif) .
.
依题意,得.files/image439.gif) 解之得
解之得.files/image441.gif) .
.
③当a<0时,.files/image430.gif) 等价于
等价于.files/image444.gif) ,即
,即.files/image446.gif) ?
?
此时.files/image033.gif) 的单调递减区间为
的单调递减区间为.files/image449.gif) ,
,.files/image451.gif) 得
得.files/image453.gif)
综上,实数a的取值范围是.files/image455.gif)
法二:.files/image457.gif)
.files/image459.gif)
由.files/image033.gif) 在区间
在区间.files/image462.gif) 上是减函数,可得
上是减函数,可得
.files/image464.gif) 在区间
在区间.files/image462.gif) 上恒成立.
上恒成立.
① 当.files/image467.gif) 时,
时,.files/image469.gif) 不合题意
不合题意
② 当.files/image471.gif) 时,可得
时,可得.files/image473.gif) 即
即.files/image475.gif)
.files/image477.gif)
.files/image479.gif)
32解:(1) 由 .files/image481.gif) 得
得.files/image483.gif)
.files/image485.gif)
.files/image487.gif)
(2) .files/image489.gif)
.files/image491.gif)
.files/image493.gif)
.files/image495.gif)
.files/image497.gif) 又
又 .files/image499.gif)
.files/image495.gif) 数列
数列.files/image273.gif) 是一个首项为
是一个首项为
.files/image502.gif) ,公比为2的等比数列;
,公比为2的等比数列;
.files/image495.gif)
.files/image504.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com