
题目列表(包括答案和解析)
10.定义在 上的偶函数
上的偶函数 ,当
,当 时,
时, 若存在
若存在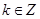 ,使方程
,使方程 的实数根
的实数根 ,则
,则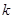 的取值集合是
( )
的取值集合是
( )
A.{0} B.{-3} C.{-4,0} D.{-3,0}
偶函数 满足
满足 ,且在区间[0,3]与
,且在区间[0,3]与 上分别递减和递增,则不等式
上分别递减和递增,则不等式 的解集为( )
的解集为( )
A. B.
B.
C. D.
D.
若函数![]() ,则下列结论正确的是 ( )
,则下列结论正确的是 ( )
A." ![]() ,
,![]() 在(0,+¥)上是增函数
在(0,+¥)上是增函数
B." ![]() ,
,![]() 在(0,+¥)上是减函数
在(0,+¥)上是减函数
C.$ ![]() ,
,![]() 是偶函数
是偶函数
D.$ ![]() ,
,![]() 是奇函数
是奇函数
设![]() 是R上的偶函数,且在(0,+∞)上是减函数,若x1<0且x1+x2>0,则( )
是R上的偶函数,且在(0,+∞)上是减函数,若x1<0且x1+x2>0,则( )
A.f(-x1)>f(-x2) B.f(-x1)=f(-x2)
C.f(-x1)<f(-x2) D.f(-x1)与f(-x2)大小不确定
偶函数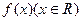 满足
满足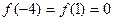 ,且在区间[0,3]与
,且在区间[0,3]与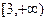 上分别递减和递增,则不等式
上分别递减和递增,则不等式 的解集为( )
的解集为( )
A.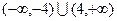 | B.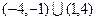 |
C.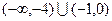 | D. |
一、
1.C 2.D 3.B 4.C 5.B 6.D 7.D 8.C 9.C 10.B 11.C 12.A
二、13. 14. 15. 16.72
三、
17.(I)证明:取BD中点M,连结MC,FM,
∵F为BD1中点, ∴FM∥D1D且FM=D1D
又EC=CC1,且EC⊥MC,
∴四边形EFMC是矩形 ∴EF⊥CC1
又CM⊥面DBD1 ∴EF⊥面DBD1
∵BD1面DBD1,
∴EF⊥BD1 故EF为BD1与CC1的公垂线
(II)解:连结ED1,有V
由(I)知EF⊥面DBD1,设点D1到面BDE的距离为d,
则S△DBC?d=S△DCD?EF.
∵AA1=2?AB=1.
故点D1到平面BDE的距离为.
18.解:设z=
由题设
即
(舍去)
即|z|=
19.(I)解∵
(II)证明:由已知
=
所以
20.解(I)
所以函数的最小正周期为π,最大值为.
(Ⅱ)由(Ⅰ)知
1
1
1
21.解:如图建立坐标系:以O为原点,正东方向为x轴正向.
在时刻:t(h)台风中心的坐标为
此时台风侵袭的区域是,
其中t+60,
若在t时,该城市O受到台风的侵袭,则有
即
即, 解得.
答:12小时后该城市开始受到台风气侵袭
22.解:根据题设条件,首先求出点P坐标满足的方程,据此再判断是否存在两定点,使得
点P到定点距离的和为定值.
按题意有A(-2,0),B(2,0),C(2,4a),D(-2,4a)
设,
由此有E(2,4ak),F(2-4k,4a),G(-2,4a-4ak).
直线OF的方程为:, ①
直线GE的方程为:. ②
从①,②消去参数k,得点P(x,y)坐标满足方程,
整理得.
当时,点P的轨迹为圆弧,所以不存在符合题意的两点.
当时,点P轨迹为椭圆的一部分,点P到该椭圆焦点的距离的和为定长.
当时,点P到椭圆两个焦点的距离之和为定值.
当时,点P到椭圆两个焦点的距离之
和为定值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com