
题目列表(包括答案和解析)



 的通项公式;
的通项公式; ,若
,若 对
对 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 为首项,公比为
为首项,公比为 的数列
的数列 ,
, ,使得数列
,使得数列 中每一项都是数列
中每一项都是数列 中不同的项,若存在,求出所有满足条件的数列
中不同的项,若存在,求出所有满足条件的数列 的通项公式;若不存在,说明理由
的通项公式;若不存在,说明理由数列![]() 的通项公式
的通项公式![]()
![]()
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述结果推测出计算f(n)的公式,并用数学归纳法加以证明.
求通项公式:
(1)
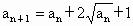 ,
,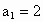 ;求
;求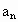 .
.
(2)
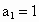 ,
,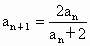 ,求
,求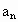 .
.
(3)
设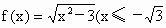 ,数列
,数列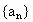 在n≥2时满足
在n≥2时满足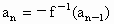
,
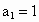 ,求
,求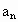 .
.
求通项公式:
(1)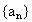 的各项均为正数,且满足关系
的各项均为正数,且满足关系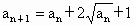 ,
,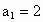 ;求
;求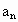 .
.
(2)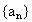 中,
中,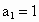 ,
,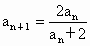 ,求
,求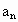 .
.
(3)设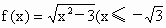 ,数列
,数列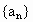 在n≥2时满足
在n≥2时满足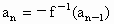
,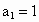 ,求
,求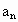 .
.
| 1 |
| (n+1)2 |
| n |
| 2 |
一、选择题:
1.B 2.D 3.A 4.A 5.A 6.B 7.B 8.B 9.C 10.C
二、填空题:
11..files/image261.gif) 12.
12..files/image263.gif) 13.
13..files/image265.gif) 14.
14..files/image267.gif) 15.
15..files/image269.gif) 16.
16..files/image271.gif) 17.
17. .files/image273.gif) 18.
18..files/image275.gif) 19.
19..files/image277.gif) 20.1)、5)
21.
20.1)、5)
21..files/image279.gif) 22.
22..files/image281.gif) 23.3)4) 24.3
23.3)4) 24.3
三、解答题:
25解:(Ⅰ) .files/image283.gif) ……2分
……2分
.files/image285.gif)
.files/image287.gif) .
.
.files/image289.gif) 的最小正周期是
的最小正周期是.files/image122.gif) .
.
(Ⅱ) ∵.files/image292.gif) ,
,
∴.files/image294.gif) .
.
∴当.files/image296.gif) 即
即.files/image298.gif) 时,函数
时,函数.files/image114.gif) 取得最小值是
取得最小值是.files/image301.gif) .
.
∵.files/image303.gif) ,
,
∴.files/image305.gif) .
.
26解:(1)∵.files/image177.gif) ,∴
,∴.files/image307.gif) ,即
,即.files/image309.gif) .
.
∴.files/image311.gif) .
.
由.files/image313.gif) ,得
,得.files/image315.gif) 或
或.files/image317.gif) ;
;
由.files/image319.gif) ,得
,得.files/image321.gif) .因此,
.因此,
函数.files/image181.gif) 的单调增区间为
的单调增区间为.files/image323.gif) ,
,.files/image325.gif) ;单调减区间为
;单调减区间为.files/image327.gif) .
.
.files/image181.gif) 在
在.files/image329.gif) 取得极大值为
取得极大值为.files/image331.gif) ;
;.files/image181.gif) 在
在.files/image333.gif) 取得极小值为
取得极小值为.files/image335.gif) .
.
由∵.files/image337.gif) ,
,.files/image339.gif) 且
且.files/image341.gif)
.files/image343.gif)
∴.files/image181.gif) 在[-
在[-.files/image183.gif) ,1]上的的最大值为
,1]上的的最大值为.files/image339.gif) ,最小值为
,最小值为.files/image346.gif) .
.
(2) ∵.files/image348.gif) ,∴
,∴.files/image350.gif) .
.
∵函数.files/image181.gif) 的图象上有与
的图象上有与.files/image185.gif) 轴平行的切线,∴
轴平行的切线,∴.files/image352.gif) 有实数解.
有实数解.
∴.files/image354.gif) ,∴
,∴.files/image356.gif) ,即
,即
.files/image358.gif) .
.
因此,所求实数.files/image173.gif) 的取值范围是
的取值范围是.files/image360.gif) .
.
27解:(1)在.files/image362.gif) 中,
中,.files/image364.gif) ,
,.files/image366.gif)
而PD垂直底面ABCD,.files/image368.gif)
.files/image370.gif) ,
,
在.files/image372.gif) 中,
中,.files/image374.gif) ,即
,即.files/image372.gif) 为以
为以.files/image376.gif) 为直角的直角三角形。
为直角的直角三角形。
.files/image377.gif) 设点
设点.files/image379.gif) 到面
到面.files/image381.gif) 的距离为
的距离为.files/image383.gif) ,
,
由.files/image385.gif) 有
有.files/image387.gif) ,
,
即 .files/image389.gif) ,
,
.files/image391.gif) ;
;
(2).files/image393.gif) ,而
,而.files/image395.gif) ,
,
即.files/image397.gif) ,
,.files/image399.gif) ,
,.files/image401.gif) ,
,.files/image403.gif) 是直角三角形;
是直角三角形;
(3).files/image405.gif) 时
时.files/image407.gif) ,
,.files/image409.gif) ,
,
即.files/image411.gif) ,
,
.files/image403.gif) 的面积
的面积.files/image414.gif)
28解:(I)因为,.files/image416.gif) 成立,所以:
成立,所以:.files/image418.gif) ,
,
由:.files/image420.gif) ,得
,得
.files/image422.gif) ,
,
由:.files/image424.gif) ,得
,得
.files/image426.gif)
解之得:.files/image428.gif) 从而,函数解析式为:
从而,函数解析式为:.files/image430.gif)
(2)由于,.files/image432.gif) ,设:任意两数
,设:任意两数
.files/image434.gif) 是函数
是函数.files/image114.gif) 图像上两点的横坐标,则这两点的切线的斜率分别是:
图像上两点的横坐标,则这两点的切线的斜率分别是:.files/image437.gif)
又因为:.files/image439.gif) ,所以,
,所以,.files/image441.gif) ,得:
,得:.files/image443.gif)
知:
.files/image445.gif)
故,当.files/image238.gif) 是函数
是函数.files/image114.gif) 图像上任意两点的切线不可能垂直
图像上任意两点的切线不可能垂直
29解:(1)∵.files/image449.gif) ∴
∴.files/image451.gif)
两式相减得:.files/image453.gif) ∴
∴.files/image455.gif)
又.files/image457.gif) 时,
时,.files/image459.gif) ∴
∴.files/image461.gif)
∴.files/image240.gif) 是首项为
是首项为.files/image463.gif) ,公比为
,公比为.files/image463.gif) 的等比数列
的等比数列
∴.files/image466.gif)
(2).files/image468.gif)
.files/image470.gif)
.files/image472.gif)
以上各式相加得:.files/image474.gif)
.files/image476.gif)
30解:(1).files/image478.gif)
.files/image480.gif)
(2)由.files/image482.gif)
由.files/image484.gif)
.files/image486.gif)
.files/image488.gif)
.files/image490.gif)
.files/image492.gif)
.files/image494.gif) ,
,
.files/image496.gif)
.files/image498.gif)
由此得.files/image500.gif)
.files/image502.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com