
题目列表(包括答案和解析)
给出下列命题:
①若函数![]() 的反函数是它本身,则a=0;
的反函数是它本身,则a=0;
②当a>1时,函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和不可能为a;
③设f(x)是定义在R上的连续函数,若不等式f(x)<0的解集为(1,2),则不等式f(x-1)<0的解集为(2,3).
填出你认为正确的所有命题序号________.
给出下列命题:
①若函数![]() 的反函数是它本身,则a=0;
的反函数是它本身,则a=0;
②当a>1时,函数f(x)=ax+loga(x+1)在[0,1]上的最大值与最小值之和不可能为a;
③设f(x)是定义在R上的连续函数,若不等式f(x)<0的解集为(1,2),则不等式f(x-1)<0的解集为(2,3).
填出你认为正确的所有命题序号________.
①若函数y=![]() (-1≤x≤a)的反函数是它本身,则a=0;
(-1≤x≤a)的反函数是它本身,则a=0;
②当a>1时,函数f(x)=ax+loga(x十1)在[0,1]上的最大值与最小值之和不可能为a;
③设f(x)是定义在R上的连续函数,若不等式f(x)<0的解集为(1,2),则不等式f(x—1)<0的解集为(2,3).
填出你认为正确的所有命题序号_____________.
现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率;
(Ⅲ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记 ,求随机变量
,求随机变量 的分布列与数学期望
的分布列与数学期望 .
.
【解析】依题意,这4个人中,每个人去参加甲游戏的概率为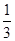 ,去参加乙游戏的概率为
,去参加乙游戏的概率为 .
.
设“这4个人中恰有i人去参加甲游戏”为事件

则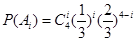 .
.
(1)这4个人中恰有2人去参加甲游戏的概率
(2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B,则 .由于
.由于 互斥,故
互斥,故
所以,这个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为 .
.
(3) 的所有可能取值为0,2,4.由于
的所有可能取值为0,2,4.由于 互斥,
互斥, 互斥,故
互斥,故
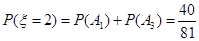

所以 的分布列是
的分布列是
|
|
0 |
2 |
4 |
|
P |
|
|
|
随机变量 的数学期望
的数学期望 .
.
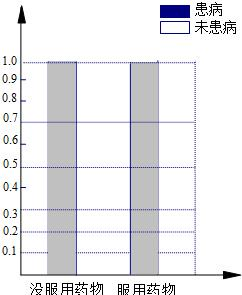
| 38 |
| 9 |

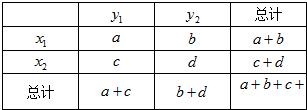
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com