题目列表(包括答案和解析)
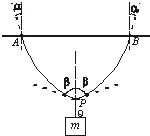
如图所示，一根均质绳质量为M，其两端固定在天花板上的A、B两点，在绳的中点悬挂一重物，质量为m，悬挂重物的绳PQ质量不计．设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角，则| tanα |
| tanβ |
如图所示，一根均质绳质量为M，其两端固定在天花板上的A、B两点，在绳的中点悬挂一重物，质量为m，悬挂重物的绳PQ质量不计．设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角，则| tanα | tanβ |
如图所示，一根均质绳质量为M，其两端固定在天花板上的A、B两点，在绳的中点悬挂一重物，质量为m，悬挂重物的绳PQ质量不计。设α、β分别为绳子端点和中点处绳子的切线方向与竖直方向的夹角，则
等于
A． 
B．
C．
D．
| tanα |
| tanβ |
A．
| B．
| C．
| D．
|
等于（ ）
1. 1、1
2. 0、2/3
3.qEl 
5. 
6. D 7. B 8. A 9. C 10. D
11. AC 12. AC 13. BD 14. ABD
15. (1)×1Ω档、先调零 （2）1300Ω、5.4mA、27V
16．D 17. （1）如右图（2）3 （3）cbadfe
18. 匀速直线运动、
19. （1） ①③②④ （2）D （3）
，
是n个点对应的圆心角，T为打点时间间隔（4）没有影响
20. 解：
（1）气体做等压变化：
（2分）
，得
（1分）
℃（1分）
（2）设转到180°时水银不溢出，
，
，
，所以水银将溢出（2分）
设转到180°时水银长度为
有:
（2分）
解得：
（1分）
设转到240°时，气体长度为
（2分）
解得
（1分）
21.解：
过O点作竖直线OE，由题意，木板的重心在E点（2分）
（3分）
加上小物块，木板水平后，由力矩平衡可知：
（3分）
解得： M=
（2分）
（若有同学利用几何关系，得到一含15°的复杂关系式，不要直接批错，批改时请用计算器确认其答案是否正确）
22. 解：
（1）线圈在只有一条边在磁场中时，感应电流最大：
等效切割速度为
（1分）
（1分）
从OQ边进入磁场转180°，到将要再次进入磁场时为一个周期，所以：
（2分）
（2）电流最大时，安培力最大，此时所需要的推力最大
由线框匀速转动可知力矩平衡：
，（1分）
解出
（1分）
在一个周期内外力不为零时力的作用点转过的弧长为：
（1分）
外力做的功为：
=
（2分）
（也可用电流做功来求解）
（3）如图所示：（3分）
23.解：
（1）对木板进行受力分析，由牛顿第二定律可得：
（2分）
解得：
（1分）
（2）木板前进8米时与
分离：
（2分）
可得：
（2分）
（3）从开始到木板停止：
（3分）
解出
木板的运动距离为
（2分）
（也可用牛顿定律解）
24.解：（1）该同学的解法是错误的。（2分）
在B点虽然速度为零，但并不处于平衡状态。（2分）
由能量守恒：
----------①
或
----------②
可得：
（2分）
（写出方程①或②，即可得这2分）
（2）m运动到C点时，在沿绳方向的速度为0，所以此时M速度为0（2分）
（2分）
由
解出
（2分）
（3）M向下先加速、再减速到零、然且向上加速、再减速到零。（2分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com