
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: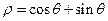 和直线
和直线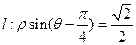 ,
,
(1)求圆O和直线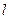 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线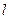 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数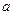
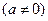 和
和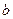 ,不等式
,不等式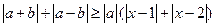 恒成立,试求实数
恒成立,试求实数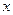 的取值范围.
的取值范围.
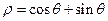 和直线
和直线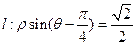 ,
,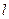 的直角坐标方程;(2)当
的直角坐标方程;(2)当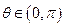 时,求直线
时,求直线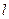 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.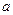
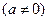 和
和 ,不等式
,不等式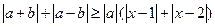 恒成立,试求实数
恒成立,试求实数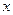 的取值范围.
的取值范围.C
[解析] 由基本不等式,得ab≤![]() =
=![]() =
=![]() -ab,所以ab≤
-ab,所以ab≤![]() ,故B错;
,故B错;![]() +
+![]() =
=![]() =
=![]() ≥4,故A错;由基本不等式得
≥4,故A错;由基本不等式得![]() ≤
≤![]() =
=![]() ,即
,即![]() +
+![]() ≤
≤![]() ,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×
,故C正确;a2+b2=(a+b)2-2ab=1-2ab≥1-2×![]() =
=![]() ,故D错.故选C.
,故D错.故选C.
.定义域为R的函数 满足
满足 ,且当
,且当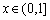 时,
时, ,则当
,则当 时,
时,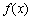 的最小值为( )
的最小值为( )
(A) (B)
(B)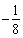 (C)
(C)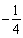 (D)
(D)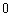
.过点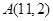 作圆
作圆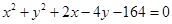 的弦,其中弦长为整数的共有 ( )
的弦,其中弦长为整数的共有 ( )
A.16条 B. 17条 C. 32条 D. 34条
一、选择题:DDBD CCBA
二、填空题:9、.files/image217.gif) 10、-2 11、1 12、11
10、-2 11、1 12、11
13、解析: .files/image173.gif)
.files/image219.gif) 14、
14、.files/image221.gif)
15、解:(Ⅰ).files/image223.gif) 时,f(x)>1
时,f(x)>1
令x=-1,y=0则f(-1)=f(-1)f(0)∵f(-1)>1
∴f(0)=1
若x>0,则f(x-x)=f(0)=f(x)f(-x)故.files/image225.gif)
故x∈R f(x)>0
任取x1<x2 .files/image227.gif)
.files/image229.gif)
故f(x)在R上减函数
(Ⅱ)①.files/image231.gif) 由f(x)单调性
由f(x)单调性
an+1=an+2 故{an}等差数列 .files/image233.gif)
②.files/image235.gif)
.files/image237.gif)
.files/image239.gif) 是递增数列
是递增数列
当n≥2时,.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
即.files/image247.gif)
而a>1,∴x>1
故x的取值范围(1,+∞)
16、解:(I).files/image249.gif) ,
,
令.files/image251.gif) (舍去)
(舍去)
.files/image253.gif) 单调递增;
单调递增;
当.files/image255.gif) 单调递减.
单调递减.
.files/image257.gif) 上的极大值
上的极大值
(II)由.files/image259.gif) 得
得
.files/image261.gif) , …………①
, …………①
设.files/image263.gif) ,
,
.files/image265.gif) ,
,
依题意知.files/image267.gif) 上恒成立,
上恒成立,
.files/image269.gif) ,
,
.files/image271.gif) ,
,
.files/image273.gif) 上单增,要使不等式①成立,
上单增,要使不等式①成立,
当且仅当.files/image275.gif)
(III)由.files/image277.gif)
令.files/image279.gif) ,
,
当.files/image281.gif) 上递增;
上递增;
当.files/image283.gif) 上递减
上递减
而.files/image285.gif) ,
,
.files/image287.gif) 恰有两个不同实根等价于
恰有两个不同实根等价于
.files/image289.gif)
.files/image291.gif)
17、解:(Ⅰ)由题可得.files/image293.gif) .
.
所以曲线.files/image057.gif) 在点
在点.files/image296.gif) 处的切线方程是:
处的切线方程是:.files/image298.gif) .
.
即.files/image300.gif) .
.
令.files/image302.gif) ,得
,得.files/image304.gif) .即
.即.files/image306.gif) .显然
.显然.files/image308.gif) ,∴
,∴.files/image310.gif) .
.
(Ⅱ)由.files/image310.gif) ,知
,知.files/image312.gif) ,同理
,同理.files/image314.gif) .
.
故.files/image316.gif) .
.
从而.files/image318.gif) ,即
,即.files/image320.gif) .所以,数列
.所以,数列.files/image215.gif) 成等比数列.
成等比数列.
故.files/image322.gif) .即
.即.files/image324.gif) .
.
从而.files/image326.gif) 所以
所以.files/image328.gif)
(Ⅲ)由(Ⅱ)知.files/image328.gif) ,
,
∴.files/image330.gif) ∴
∴.files/image332.gif)
当.files/image334.gif) 时,显然
时,显然.files/image336.gif) .
.
当.files/image338.gif) 时,
时,.files/image340.gif)
∴.files/image342.gif)
.files/image344.gif)
.files/image346.gif)
.files/image348.gif) .
.
综上,.files/image350.gif)
.files/image352.gif) .
.
18、解:(I).files/image249.gif) ,
,
令.files/image251.gif) (舍去)
(舍去)
.files/image253.gif) 单调递增;
单调递增;
当.files/image255.gif) 单调递减.
单调递减.
.files/image257.gif) 上的极大值
上的极大值
(II)由.files/image259.gif) 得
得
.files/image261.gif) , …………①
, …………①
设.files/image263.gif) ,
,
.files/image265.gif) ,
,
依题意知.files/image267.gif) 上恒成立,
上恒成立,
.files/image269.gif) ,
,
.files/image271.gif) ,
,
.files/image273.gif) 上单增,要使不等式①成立,
上单增,要使不等式①成立,
当且仅当.files/image275.gif)
(III)由.files/image277.gif)
令.files/image279.gif) ,
,
当.files/image281.gif) 上递增;
上递增;
当.files/image283.gif) 上递减
上递减
而.files/image285.gif) ,
,
.files/image287.gif) 恰有两个不同实根等价于
恰有两个不同实根等价于
.files/image289.gif)
.files/image291.gif)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com