题目列表(包括答案和解析)
已知等差数列
的首项为1，公差为d，等比数列
的首项为1，公比为q.集合A=
，若A=B则q的值是 .
已知等差数列
的首项为a，公差为b；等比数列
的首项为b，公比为a，其中a，
，且
．
（1）求a的值；
（2）若对于任意
，总存在
，使
，求b的值；
（3）在（2）中，记
是所有中满足， 的项从小到大依次组成的数列，又记
为的前n项和，
的前n项和，求证：≥
已知等差数列
的首项为a，公差为b，等比数列
的首项为b，公比为a，其中a，b都是大于1的正整数，且
．
（1）求a的值；
（2）若对于任意的
，总存在
，使得
成立，求b的值；
（3）令
，问数列
中是否存在连续三项成等比数列？若存在，求出所有成等比数列的连续三项；若不存在，请说明理由．
已知等差数列
的首项为a，公差为b，等比数列
的首项为b，公比为a，其中a、b都是大于1的正整数，且
。
①求a的值；
②对于任意的
，总存在
，使得
成立，求b；
③令
，问数列
中是否存在连续三项成等比数列，若存在，求出所有成等比数列的连续三项，若不存在，请说明理由。（14分）
已知等差数列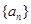
的首项为a，公差为b，等比数列
的首项为b，公比为a，其中a，b均为正整数，若
。
（1）求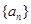、的通项公式；
（2）若
成等比数列，求数列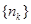
的通项公式。
（3）设
的前n项和为
，求当
最大时，n的值。
一、选择题：本大题共10个小题，每小题5分，共50分。
题号
1
2
3
4
5
6
8
9
10
答案
C
C
B
D
B
B
A
C
A
二、填空题: 本大题共7个小题，每小题4分，共28分。
11. 
12．8
13．-3＜a＜8 14．4
15．16
16．10
17．
三、解答题: 本大题共5个小题，共72分。
18．(本小题满分14分)
A={x|3
-4x-4＜0}={x|(3x+2)(x-2)＜0} ={x|-
＜x＜2} ……………………5
B={x|(3x-1)(x-1)＞0}={x|x＞1或 x＜
}
…………………9
A∩B ={x|1＜x＜2 或 -＜x＜ }
…………………12
Cu(A
)={x|x≥2或≤x≤1或x≤-} ………………….14
19．(本小题满分14分)
(1)设数列
的公比为q，由a2=8，a5=512，
可得a1q=8，a1q4=512。
解得a1=2，q=4。 ……………………4
所以数列的通项公式为
an=2×4n-1=22n-1。 ……………………7
(2)由an=22n-1，得bn=log2an=2n-1 ……………………10
所以数列
是首项b1=1，公差d=2的等差数列。
故Sn=
即数列的前n项和Sn=n2
……………………14
20．(本小题满分14分)
设楼房每平方米的平均综合费用为f(x)元，
则f(x)=(560+48x)+
=560+48x+
(x≥10，x∈N*)
...............5
f(x)≥560+2
=560+1440=2000
………….10
当且仅当48x=时，即当x=15时，f(x)取最小值f(15)=2000。……………13
答：为了楼房每平方米的平均综合费用最少，该楼房应建为15层。…………….14
21．（本小题满分15分）
(1)由余弦定理得a2+b2-ab=4。 ………………..2
又因为△ABC的面积等于
，所以
，得ab=4。………….. 4
由a2+b2-ab=4和ab=4，解得a=2，b=2。 ………………..7
(2)由正弦定理，已知条件化为b=
由a2+b2-ab=4和b=
，b=
，
……………….12
所以△ABC的面积S=
。
………………..15
22．（本小题满分15分）
(1)Sn=n2-4n+4=(n-2)2，
当n=1时，a1=S1=1； …………….2
当≥2时，an=Sn-Sn-1=(n-2)2-(n-3)2=2n-5，
 |
∴an=
1 n=1
2n-5 n≥2
………………5
(2)Tn=
，由(1)可得
Tn=-1+(-1)+
=-2+
……………10
(3)由题设可得b1=-3或bn=1-
(n≥2)，
∵b1=-3＜0，b2=1+4=5＞0，b3=-3＜0，
∴i=1，i=2都满足bi?bi+1＜0
∵当n≥3时，bn+1-bn=
＞0，
即当n≥3时，数列递增。
∵b4=-
＜0，由1-＞0
n≥5，可知i=4满足bi?bi+1＜0，
∴数列的变号数为3。
………………15
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com