
题目列表(包括答案和解析)
 ,带电量为
,带电量为 ,置于光滑绝缘水平面上的A点。当空间存在着斜向上的匀强电场时,该小球从静止开始始终沿水平面做匀加速直线运动,当运动到B点时,测得其速度
,置于光滑绝缘水平面上的A点。当空间存在着斜向上的匀强电场时,该小球从静止开始始终沿水平面做匀加速直线运动,当运动到B点时,测得其速度 ,此时小球的位移为
,此时小球的位移为 。求此匀强电场E的取值范围。(
。求此匀强电场E的取值范围。( )
) ,得
,得  =
= (1)
(1)  ,所以当
,所以当 时,小球将始始终沿水平面做匀加速直线运动。
时,小球将始始终沿水平面做匀加速直线运动。
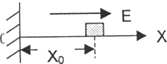
 (2006?崇明县二模)一个质量为m带有电荷为-q的小物体,可在水平轨道OX上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿OX轴正方向如图所示,小物体以速度V0从图示位置向左运动,运动时受到大小不变的摩擦力f作用,设小物体与墙壁碰撞时不损失机械能,且电量保持不变,求它停止前所通过的总路程S.
(2006?崇明县二模)一个质量为m带有电荷为-q的小物体,可在水平轨道OX上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿OX轴正方向如图所示,小物体以速度V0从图示位置向左运动,运动时受到大小不变的摩擦力f作用,设小物体与墙壁碰撞时不损失机械能,且电量保持不变,求它停止前所通过的总路程S.| v02 | 2 |
 一个质量为m带有电荷为-q的小物体,可在水平轨道OX上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿OX轴正方向如图所示,小物体以速度V从图示位置向左运动,运动时受到大小不变的摩擦力f作用,设小物体与墙壁碰撞时不损失机械能,且电量保持不变,求它停止前所通过的总路程S.
一个质量为m带有电荷为-q的小物体,可在水平轨道OX上运动,O端有一与轨道垂直的固定墙.轨道处于匀强电场中,场强大小为E,方向沿OX轴正方向如图所示,小物体以速度V从图示位置向左运动,运动时受到大小不变的摩擦力f作用,设小物体与墙壁碰撞时不损失机械能,且电量保持不变,求它停止前所通过的总路程S. 上述解法正确吗?若你认为是正确的话,则解出其结果,若你认为不正确的话,则列式解出你认为正确的结果.
上述解法正确吗?若你认为是正确的话,则解出其结果,若你认为不正确的话,则列式解出你认为正确的结果.| v02 |
| 2 |
 如图所示,AB和BC是由相同材料组成的绝缘斜面和水平面,A与C的水平距离为SAC=5米,H高2.8米,h=0.8米.质量为m的小滑块由A静止开始释放,它恰能运动到C而静止.现在让小滑块带上电量q,并在轨道所在处施加竖直向下的匀强电场,场强大小E=mg/2q,在A点给小滑块一个沿斜面向下的4米/秒的初速度,求滑块滑出C后所抛出的水平距离是多大?
如图所示,AB和BC是由相同材料组成的绝缘斜面和水平面,A与C的水平距离为SAC=5米,H高2.8米,h=0.8米.质量为m的小滑块由A静止开始释放,它恰能运动到C而静止.现在让小滑块带上电量q,并在轨道所在处施加竖直向下的匀强电场,场强大小E=mg/2q,在A点给小滑块一个沿斜面向下的4米/秒的初速度,求滑块滑出C后所抛出的水平距离是多大?| 1 |
| 2 |
|
| g(H-h)+v02 |
| 1 |
| 2 |
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com