
题目列表(包括答案和解析)
椭圆 的右焦点为
的右焦点为 ,右准线为
,右准线为 ,离心率为
,离心率为 ,点
,点 在椭圆上,以
在椭圆上,以 为圆心,
为圆心, 为半径的圆与
为半径的圆与 的两个公共点是
的两个公共点是 .
.

(1)若 是边长为
是边长为 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;
(2)若 三点在同一条直线
三点在同一条直线 上,且原点到直线
上,且原点到直线 的距离为
的距离为 ,求椭圆方程.
,求椭圆方程.
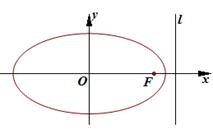
椭圆 的右焦点为
的右焦点为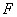 ,右准线为
,右准线为 ,离心率为
,离心率为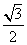 ,点
,点 在椭圆上,以
在椭圆上,以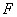 为圆心,
为圆心, 为半径的圆与
为半径的圆与 的两个公共点是
的两个公共点是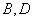 .
.
(1)若 是边长为
是边长为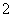 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;
(2)若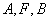 三点在同一条直线
三点在同一条直线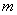 上,且原点到直线
上,且原点到直线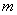 的距离为
的距离为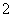 ,求椭圆方程.
,求椭圆方程.
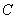 的右焦点为
的右焦点为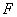 ,右准线为
,右准线为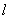 ,离心率为
,离心率为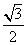 ,点
,点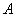 在椭圆上,以
在椭圆上,以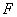 为圆心,
为圆心,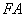 为半径的圆与
为半径的圆与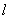 的两个公共点是
的两个公共点是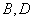 .
.
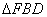 是边长为
是边长为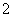 的等边三角形,求圆的方程;
的等边三角形,求圆的方程;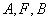 三点在同一条直线
三点在同一条直线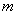 上,且原点到直线
上,且原点到直线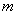 的距离为
的距离为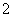 ,求椭圆方程.
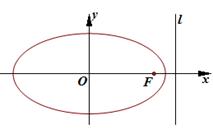
,求椭圆方程.以椭圆![]() 的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是
的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
以椭圆![]() 的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是
的右焦点F为圆心,a为半径的圆与椭圆的右准线交于不同的两点,则该椭圆的离心率的取值范围是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
1、D 2、B 3、D 4、C 5、A 6、B 7、C 8、D 9、C 10、A
11、16; 12、; 13、120; 14、; 15、0或4; 16、
17、,,
,
,得,又,或
当,即时,
18、(1),又,
(2)连结,交于点,,又,面面
,,是二面角的平面角,不妨设
则,,,,中,
二面角的大小为
(3)假设棱上存在点,由题意得,要使,只要即可
当时,中,,
,时,
19、(1)设动点,,,,直线的方程为
,,点的轨迹的方程是
(2)设,,。
同理,是方程的两个根,
,
20、(1)由题意得
(2)当时,,
当时,
时上式成立。
当时,
当时,
当第个月的当月利润率
当时,是减函数,此时的最大值为
当时,
当且仅当时,即时,,又,
当时,
答:该企业经销此产品期间,第40个月的当月利润率最大,最大值为
21、(1)
(2) ①
又 ②
由(1)知,,……
①+②得:,
(3)为增函数,时,
由(1)知函数的图象关于点对称,记点,
所求封闭图形的面积等于的面积,即,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com