练习册

  • 练习册
  • 试题
    C．OP两点间的距离为 D．OP两点间的距离为 2,4,6 A．地球绕太阳运行的周期和地球到太阳中心的距离 B．地球绕太阳运行的周期和地球的半径 C．月球绕地球运行的周期和地球的半径 D．月球绕地球运行的周期和月球到地球中心的距离 【查看更多】

     

    题目列表(包括答案和解析)

    （1）如图甲所示，O点为振源．OP距离为s．t=0时刻，O点从平衡位置开始向下负方向）振动，产生向右沿直线传播的简谐横波，图乙为P点的振动图象（从t1时刻开始振动）．则______．（填入正确选项前的字母）

    A．该波的频率为
    B．t2时刻P点的速度最大，方向沿y正方向
    C．这列波的波长为
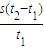
    D．若t2时刻O点处于负最大位移处，则s可能是波长的倍
    （2）如图丙所示，半圆形玻璃砖的半径R=10cm，折射率，直径AB与屏MN垂直并接触于A点，一细束单色光a以入射角θ1=30°沿半径射向玻璃砖的圆心O，在屏MN上出现了两个光斑．求这两个光斑间的距离L．

    查看答案和解析>>

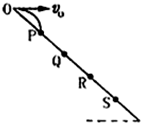    如图所示，斜面上O、P、Q、R、S五个点，距离关系为
    .
    OP
    =
    .
    PQ
    =
    .
    QR
    =
    .
    RS
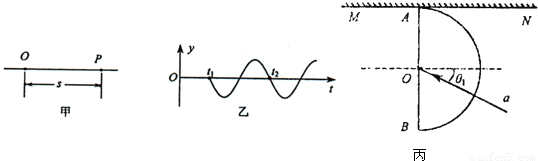
    ，从O点以υ0的初速度水平抛出一个小球，不计空气阻力，小球落在斜面上的P点．若小球从O点以2υ0的初速度水平抛出，则小球将落在斜面上的（　　）

    查看答案和解析>>

    水平放置的两块平行金属板长L＝5.0 cm，两板间距d＝1.0 cm，两板间电压为90 v，且上板为正，一个电子沿水平方向以速度v0＝2.0×107 m/s，从两板中间射入，如图．已知电子的电量为1.6×10－19 C，质量为9.1×10－31 kg求：

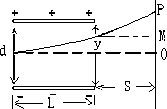
    (1)电子偏离金属板时的侧位移是多少？

    (2)电子离开电场后，打在屏上的P点，若S＝10 cm，求OP的长？

    查看答案和解析>>

    在“验证动量守恒定律”实验中
    ①下列做法正确的是                。
    A．斜槽轨道必须光滑   
    B．斜槽轨道末端点的切线可以不水平   
    C．应让入射小球每次从斜槽上相同的位置自由滑下
    D．需要的测量工具是天平、刻度尺和游标卡尺
    E．重复实验10次后用尽可能小的圆把所有落点圈在里面，其圆心就是各小球落点的平均位置    

    ②如图，O为挂在斜槽边缘的重垂线在白纸上所指的位置，M  P、N为两小球实验后得到的落点的平均位置，两小球质量ml、m2且m1>m2。测得OM,OP、ON间的距离分别为Sl、S2、S3，则验证动量守恒定律是否成立的表达式为                 (用m1、m2、S1、S2、S3表示)。

    查看答案和解析>>

    如图1所示，用“碰撞试验器”可以验证动量守恒定律，即研究两个小球在轨道水平部分碰撞前后的动量关系．

    （1）试验中，直接测定小球碰撞前后的速度是不容易的．但是，可以通过仅测量
    C
    C
    （填选项前的序号），间接地解决这个问题．
    A．小球开始释放高度h  B．小球抛出点距地面得高度H  C．小球做平抛运动的射程
    （2）图1中O点是小球抛出点在地面上的垂直投影．实验时，先让入射球m1多次从斜轨上S位置静止释放，找到其平均落地点的位置P，测量平抛射程OP．然后，把被碰小球m2静置于轨道的水平部分，再将入射球m1从斜轨上S位置静止释放，与小球m2相碰，并多次重复．接下来要完成的必要步骤是
    A、D、E
    A、D、E
    ．（填选项前的符号）
    A．用天平测量两个小球的质量m1、m2      
    B．测量小球m1开始释放高度h
    C．测量抛出点距地面的高度H
    D．分别找到m1、m2相碰后平均落地点的位置M、N
    E．测量平抛射程OM、ON
    （3）若两球相碰前后的动量守恒，其表达式可表示为
    m1?OM+m2?ON=m1OP
    m1?OM+m2?ON=m1OP
    （用②中测量的量表示）；若碰撞是弹性碰撞．那么还应满足的表达式为
    m1?OM2+m2?ON2=m1OP2
    m1?OM2+m2?ON2=m1OP2
    （用②中测量的量表示）．
    （4）经测定，m1=45.0g，m2=7.5g，小球落地点的平均位置距O点的距离如图2所示．碰撞前、后m1-的动量分别为p1与p1′，则p1：p1′=
    14
    14
    ：11；若碰撞结束时m2的动量为p2′，则p1′：p2′=11：
    2.9
    2.9
    ．实验结果说明，碰撞前、后总动量的比值
    P1P1′+P2′
    为
    1.01
    1.01
    ．

    查看答案和解析>>


    同步练习册答案