
题目列表(包括答案和解析)
 如图,光滑水平面上带电量为q、质量为m的小球P靠在一劲度系数为k的轻弹簧的右端.现将弹簧向左压缩长度为L后自A点静止释放小球P,小球P运动到B处时恰与静止的不带电的相同小球Q相碰并粘在一起,进入水平向右的匀强电场中.C点右侧是垂直纸面向里的匀强磁场,小球运动到C点时,电场突然变为竖直向上,但大小不变.此后物体开始在竖直平面内作圆周运动,到达最高点时撤去电场,小球正好又落回B点.已知AB=BC=L,弹簧的弹性势能与其形变量x的关系是Ep=
如图,光滑水平面上带电量为q、质量为m的小球P靠在一劲度系数为k的轻弹簧的右端.现将弹簧向左压缩长度为L后自A点静止释放小球P,小球P运动到B处时恰与静止的不带电的相同小球Q相碰并粘在一起,进入水平向右的匀强电场中.C点右侧是垂直纸面向里的匀强磁场,小球运动到C点时,电场突然变为竖直向上,但大小不变.此后物体开始在竖直平面内作圆周运动,到达最高点时撤去电场,小球正好又落回B点.已知AB=BC=L,弹簧的弹性势能与其形变量x的关系是Ep=| 1 |
| 2 |
|
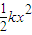 ,式中k为弹簧的劲度系数.求:
,式中k为弹簧的劲度系数.求: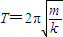 ,则小球从A出发最终落回到B点的总时间.
,则小球从A出发最终落回到B点的总时间.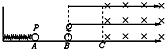
(10分)如图所示,用长L=0.50m的绝缘轻质细线,把一个质量 m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间,平行金属板间的距离d=5.0cm,两板间电压U=1.0×103V。静止时,绝缘线偏离竖直方向θ角,小球偏离竖直距离a=1.0cm。(θ角很小,为计算方便可认为tanθ ≈ sinθ,取g=10m/s2,需要求出具体数值,不能用θ角表示)求:

(1)两板间电场强度的大小;
(2)判断小球带何种电荷并计算其带电荷量;
(3)在图示位置,若将细线突然剪断,小球做何种性质的运动?求加速度a的大小。
(10分)如图所示,用长L=0.50m的绝缘轻质细线,把一个质量 m=1.0g带电小球悬挂在带等量异种电荷的平行金属板之间,平行金属板间的距离d=5.0cm,两板间电压U=1.0×103V。静止时,绝缘线偏离竖直方向θ角,小球偏离竖直距离a=1.0cm。(θ角很小,为计算方便可认为tanθ ≈ sinθ,取g=10m/s2,需要求出具体数值,不能用θ角表示)求: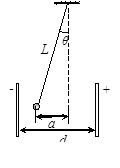
(1)两板间电场强度的大小;
(2)判断小球带何种电荷并计算其带电荷量;
(3)在图示位置,若将细线突然剪断,小球做何种性质的运动?求加速度a的大小。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com