
题目列表(包括答案和解析)
解析 以A小球为研究对象有:TAcos θ1=mAg,TA sin θ1=FBA,以B小球为研究对象有:TBcos θ2=mBg,TBsin θ2=FAB,且FAB=FBA、因θ1>θ2,故TB>TA,而cos θ2>cos θ1,故mB>mA,选项A正确.因A、B两球摆到最低点时:A小球下降的高度hA大于B小球下降的高度hB.由![]() mv2=mgh有v=
mv2=mgh有v= ![]() ,所以vA>vB,故选项C正确.由库仑定律FAB=
,所以vA>vB,故选项C正确.由库仑定律FAB=![]() ,故无法确定qA和qB的大小,选项B错误.EkA=
,故无法确定qA和qB的大小,选项B错误.EkA=![]() mAv
mAv![]() =mAgLA(1-cos θ1)=FABLA
=mAgLA(1-cos θ1)=FABLA![]() =FABLAcos θ1tan
=FABLAcos θ1tan![]() ,同理:EkB=FABLBcos θ2tan
,同理:EkB=FABLBcos θ2tan ![]() ,LAcos θ1=LBcos θ2,又θ1>θ2,所以tan
,LAcos θ1=LBcos θ2,又θ1>θ2,所以tan ![]() >tan
>tan ![]() ,即EkA>EkB,故选项D正确.
,即EkA>EkB,故选项D正确.
答案 ACD
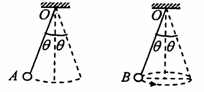
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com