练习册

  • 练习册
  • 试题
    A．HA=HB=HC B．HA＞HB＞HCC．HA＝HB＞HC D．HA＞HB＝HC第Ⅱ卷 【查看更多】

     

    题目列表(包括答案和解析)

    （2007?厦门模拟）用如图所示装置验证动量守量定律，质量为mA的钢球A用细线悬挂于点O，质量为mB的钢球B放在离地面高度为h的小支柱N上，O点到A球球心的距离为l，使悬线在A球释放前张紧，且线与竖直线的夹角为α，A球释放后摆到最低点时恰好与B球正碰，碰撞后，A球把轻质指针OC推移到与竖直线夹角β处，B球落到地面上，地面上铺一张盖有复写纸的白纸D．保持α不变，多次重复上述实验，白纸上记录了多种B球的落点，图中s是B球初始位置到落点的水平位移．
    （1）为了验证两球碰撞过程中动量守恒，某同学测得A球质量mA，B球质量mB，高度h，水平位移s，夹角α，还应测得
    夹角β
    夹角β
    、
    线长l
    线长l
    等物理量．
    （2）用测量的物理量表示碰撞前后A球、B球的动量：PA=
    mA
    		2gl(1-cosα)
    mA
    		2gl(1-cosα)
    ，PA′=
    mA
    		2gl(1-cosβ)
    mA
    		2gl(1-cosβ)
    ，PB=
    0
    0
    ，PB′
    mBs
    g
    2h
    mBs
    g
    2h
    ．

    查看答案和解析>>

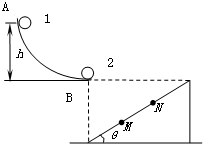    如图所示，光滑的弯曲轨道AB的末端水平，小球1从轨道上A点由静止开始下滑，与静止在末端B处的小球2发生弹性正碰，小球2抛出后落在斜面上．已知两小球质量相等，斜面的倾角为θ，A点与轨道末端B点的高度差为h，斜面底端在抛出点B的正下方，斜面顶端与抛出点在同一水平面上，斜面长度为L，斜面上M、N两点将斜面长度等分成3段，两小球都可以看作质点，一切阻力不计．求：
    （1）小球2从B点飞出时的速度大小．
    （2）为使小球2能落在M点以上（含M点），小球1开始释放的位置相对于抛出点B的高度h应满足什么条件？

    查看答案和解析>>

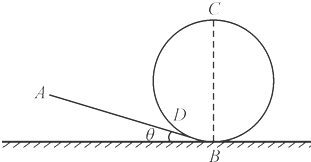    如图所示为摩托车特技比赛用的部分赛道，由一段倾斜坡道AB与竖直圆形轨道BCD衔接而成，衔接处平滑过渡且长度不计．已知坡道的倾角θ=11.5°，圆形轨道的半径R=10m，摩托车及选手的总质量m=250kg，摩托车在坡道行驶时所受阻力为其重力的0.1倍．摩托车从坡道上的A点由静止开始向下行驶，A与圆形轨道最低点B之间的竖直距离h=5m，发动机在斜坡上产生的牵引力F=2 750N，到达B点后摩托车关闭发动机．已知sin11.5°=
    15
    ，g取10m/s2，求：
    （1）摩托车在AB坡道上运动的加速度；
    （2）摩托车运动到圆轨道最低点时对轨道的压力；
    （3）若运动到C点时恰好不脱离轨道，求摩托车在BC之间克服摩擦力做的功．

    查看答案和解析>>

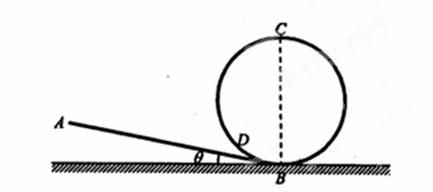
    （16分） 如图所示为摩托车特技比赛用的部分赛道，由一段倾斜坡道AB与竖直圆形轨道BCD衔接而成，衔接处平滑过渡且长度不计．已知坡道的倾角θ＝11.5°，圆形轨道的半径R＝10 m，摩托车及选手的总质量m＝250 kg，摩托车在坡道行驶时所受阻力为其重力的0.1倍．摩托车从坡道上的A点由静止开始向下行驶，A与圆形轨道最低点B之间的竖直距离h＝5 m，发动机在斜坡上产生的牵引力F＝2750 N，到达B点后摩托车关闭发动机．已知sin11.5°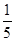＝，g取10 m/s2，求：

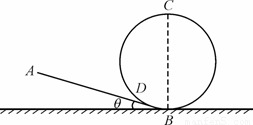
    (1) 摩托车在AB坡道上运动的加速度；

    (2) 摩托车运动到圆轨道最低点时对轨道的压力；

    (3) 若运动到C点时恰好不脱离轨道，求摩托车在BC之间克服摩擦力做的功．

     

    查看答案和解析>>

    （2013江苏省连云港市期末）如图所示为摩托车特技比赛用的部分赛道，由一段倾斜坡道AB与竖直圆形轨道BCD衔接而成，衔接处平滑过渡且长度不计。已知坡道的倾角θ=11.5°，圆形轨道的半径R=10m，摩托车及选手的总质量m=250kg，摩托车在坡道行驶时所受阻力为其重力的0.1倍。摩托车从坡道上的A点由静止开始向下行驶，A与圆形轨道最低点B之间的竖直距离h=5m，发动机在斜坡上产生的牵引力F=2750N，到达B点后摩托车关闭发动机。已知，g=10m/s2.

    (1)求摩托车在AB坡道上运动的加速度；

    (2)求摩托车运动到圆轨道最低点时对轨道的压力；

    (3)若运动到C点时恰好不脱离轨道，则摩托车在BC之间克服摩擦力做了多少功？

    查看答案和解析>>


    同步练习册答案