
题目列表(包括答案和解析)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
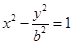 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线相交于B、C, 且
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线相交于B、C, 且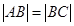 , 则双曲线M的离心率为_____________.
, 则双曲线M的离心率为_____________. 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B,C,且|AB|=|BC|,则双曲线M的离心率是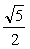



过双曲线M:![]() 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别相交于点B、C,且![]() ,则双曲线M的离心率是
,则双曲线M的离心率是
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
1-10:DCDAABCBCDC
11., 12. 85, 13. 5 ,14. 6 ,15. -3 .
1.函数的定义域是,解得x≥1,选D.
2.向量若时,∥,∴ ;时,,,选C.
3.的展开式中的系数=x3, 则实数的值是2,选D
4.过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°,则截面圆的半径是R=1,该截面的面积是π,选A.
5.若“”,则函数=在区间上为增函数;而若在区间上为增函数,则0≤a≤1,所以“”是“函数在区间上为增函数”的充分不必要条件,选A.
6.在数字1,2,3与符号“+”,“-”五个元素的所有全排列中,先排列1,2,3,有种排法,再将“+”,“-”两个符号插入,有种方法,共有12种方法,选B.
7.圆的圆心为(2,2),半径为3,圆心到到直线的距离为>3,圆上的点到直线的最大距离与最小距离的差是2R =6,选C.
8.设点P是函数的图象C的一个对称中心,若点P到图象C的对称轴上的距离的最小值,∴ 最小正周期为π,选B.
9.过双曲线的左顶点(1,0)作斜率为1的直线:y=x-1, 若与双曲线的两条渐近线分别相交于点, 联立方程组代入消元得,∴ ,x1+x2=2x1x2,又,则B为AC中点,2x1=1+x2,代入解得,∴ b2=9,双曲线的离心率e=,选D.
10.如图,OM∥AB,点P由射线OM、线段OB及AB的延长线围成的阴影区域内(不含边界).且,
由图知,x<0,当x=-时,即=-,P点在线段DE上,=,=,而<<,∴ 选C.
二.填空题:
11.; 12. 85; 13. 5 ; 14. 6 ; 15. -3 .
11.数列满足:,2,3…,该数列为公比为2的等比数列,∴ .
12.某高校有甲、乙两个数学建模兴趣班. 其中甲班有40人,乙班50人. 现分析两个班的一次考试成绩,算得甲班的平均成绩是90分,乙班的平均成绩是81分,则该校数学建模兴趣班的平均成绩是分.
13.已知,如图画出可行域,得交点A(1,2),B(3,4),则的最小值是5.
14.过三棱柱 ABC-A1B1C1 的任意两条棱的中点作直线,其中与平面ABB1A1平行的直线共有6条。
15.是偶函数,取a=-3,可得为偶函数。
16. 解 由已知条件得.
即.
解得.
由0<θ<π知,从而.
17. 解 (Ⅰ)每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的. 所以恰好有两家煤矿必须整改的概率是.
(Ⅱ)解法一 某煤矿被关闭,即该煤矿第一次安检不合格,整改后经复查仍不合格,所以该煤矿被关闭的概率是,从而煤矿不被关闭的概率是0.90.
解法二 某煤矿不被关闭包括两种情况:(i)该煤矿第一次安检合格;(ii)该煤矿第一次安检不合格,但整改后合格.
所以该煤矿不被关闭的概率是.
(Ⅲ)由题设(Ⅱ)可知,每家煤矿不被关闭的概率是0.9,且每家煤矿是否被关闭是相互独立的,所以到少关闭一家煤矿的概率是.
18. 解法一 (Ⅰ)连结AC、BD,设.
由P-ABCD与Q-ABCD都是正四棱锥,所以PO⊥平面ABCD,QO⊥平面ABCD.
从而P、O、Q三点在一条直线上,所以PQ⊥平面ABCD.
(Ⅱ)由题设知,ABCD是正方形,所以AC⊥BD.
所以
于是.
从而异面直线AQ与PB所成的角是.
(Ⅲ)由(Ⅱ),点D的坐标是(0,-,0),,
,设是平面QAD的一个法向量,由
得.
取x=1,得.
所以点P到平面QAD的距离.
解法二 (Ⅰ)取AD的中点,连结PM,QM.
因为P-ABCD与Q-ABCD都是正四棱锥,
所以AD⊥PM,AD⊥QM. 从而AD⊥平面PQM.
又平面PQM,所以PQ⊥AD.
同理PQ⊥AB,所以PQ⊥平面ABCD.
因为OA=OC,OP=OQ,所以PAQC为平行四边形,AQ∥PC.
从而∠BPC(或其补角)是异面直线AQ与PB所成的角.
因为,
所以.
从而异面直线AQ与PB所成的角是.
(Ⅲ)连结OM,则.
所以∠PMQ=90°,即PM⊥MQ.
由(Ⅰ)知AD⊥PM,所以PM⊥平面QAD. 从而PM的长是点P到平面QAD的距离.
在直角△PMO中,.
即点P到平面QAD的距离是.
19. 解 (Ⅰ)由题设知.
令.
当(i)a>0时,
若,则,所以在区间上是增函数;
若,则,所以在区间上是减函数;
若,则,所以在区间上是增函数;
(i i)当a<0时,
若,则,所以在区间上是减函数;
若,则,所以在区间上是减函数;
若,则,所以在区间上是增函数;
若,则,所以在区间上是减函数.
(Ⅱ)由(Ⅰ)的讨论及题设知,曲线上的两点A、B的纵坐标为函数的极值,且函数在处分别是取得极值,.
因为线段AB与x轴有公共点,所以.
即.所以.
故.
解得 -1≤a<0或3≤a≤4.
即所求实数a的取值范围是[-1,0)∪[3,4].
20. 解 (Ⅰ)由已知得,
.
(Ⅱ)因为,
所以.
又因为,
所以
=.
综上,.
21. 解 (Ⅰ)当AB⊥x轴时,点A、B关于x轴对称,所以m=0,直线AB的方程为
x=1,从而点A的坐标为(1,)或(1,-).
因为点A在抛物线上,所以,即.
此时C2的焦点坐标为(,0),该焦点不在直线AB上.
(Ⅱ)解法一 当C2的焦点在AB时,由(Ⅰ)知直线AB的斜率存在,设直线AB的方程为.
由消去y得. ……①
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程①的两根,x1+x2=.
所以,且
.
从而.
所以,即.
解得.
因为C2的焦点在直线上,所以.
即.
当时,直线AB的方程为;
当时,直线AB的方程为.
解法二 当C2的焦点在AB时,由(Ⅰ)知直线AB的斜率存在,设直线AB的方程
为.
由消去y得. ……①
因为C2的焦点在直线上,
所以,即.代入①有.
即. ……②
设A、B的坐标分别为(x1,y1), (x2,y2),
则x1,x2是方程②的两根,x1+x2=.
由消去y得. ……③
由于x1,x2也是方程③的两根,所以x1+x2=.
从而=. 解得.
因为C2的焦点在直线上,所以.
即.
当时,直线AB的方程为;
当时,直线AB的方程为.
解法三 设A、B的坐标分别为(x1,y1), (x2,y2),
因为AB既过C1的右焦点,又是过C2的焦点,
所以.
即. ……①
由(Ⅰ)知,于是直线AB的斜率, ……②
且直线AB的方程是,
所以. ……③
又因为,所以. ……④
将①、②、③代入④得,即.
当时,直线AB的方程为;
当时,直线AB的方程为.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com