
题目列表(包括答案和解析)
(本题14![]() 分)如图,五面体
分)如图,五面体![]()
![]() 中
中![]()
![]() ,
,![]() .底面
.底面![]() 是正三角形,
是正三角形,![]() .
.![]() 四边形
四边形![]() 是矩形
是矩形![]() ,
,![]() 二面角
二面角![]()
![]() 为直二面角.
为直二面角.
(1)![]() 在
在![]()
![]() 上运动,当
上运动,当![]() 在何处时,有
在何处时,有![]() ∥平面
∥平面![]() ,并且
,并且![]() 说明理由;
说明理由;
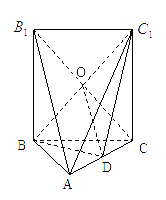
![]()
![]() (2)当
(2)当![]() ∥平面
∥平面![]() 时,求二面角
时,求二面角![]()
![]() 的
的![]() 余弦值.
余弦值.
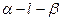 中,A、B
中,A、B ,C、D
,C、D ,ABCD为矩形,
,ABCD为矩形, 且PA=AD,M、N依次是AB、PC的中点,
且PA=AD,M、N依次是AB、PC的中点,
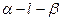 的大小(6分)
的大小(6分) (6分)
(6分) 分)如图,五面体
分)如图,五面体
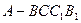 中
中
 ,
,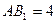 .底面
.底面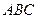 是正三角形,
是正三角形,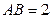 .
. 四边形
四边形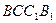 是矩形
是矩形 ,
, 二面角
二面角
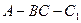 为直二面角.
为直二面角.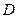 在
在
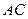 上运动,当
上运动,当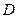 在何处时,有
在何处时,有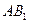 ∥平面
∥平面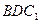 ,并且
,并且 说明理由;
说明理由;

 (2)当
(2)当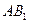 ∥平面
∥平面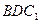 时,求二面角
时,求二面角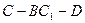
 的
的 余弦值.
余弦值.(本题满分14分)
如图,在四棱锥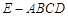 中,底面
中,底面 为矩形,平面
为矩形,平面 ⊥平面
⊥平面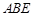 ,
,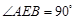 ,
,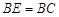 ,
,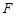 为
为 的中点,
的中点,
求证:(1)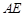 ∥平面
∥平面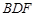 ;(2)平面
;(2)平面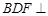 平面
平面 .
.

(本题满分14分)
 某老师从参加高一年级一次考试的学生中抽出60名学生,将其成绩(均为整数)分成六段
某老师从参加高一年级一次考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…
,…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求第四小组的频率,并补全这个频率分
布直方图;
(2)该老师不小心洒了一个墨点在直方图的
矩形区域内,求恰好落在第四组的小矩
形内的概率 (不计墨点大小);
(3)若60分及以上为及格,估计从高一年级
及格的学生中抽取一位学生分数不低于
80分的概率.
11.70 12. 2 13. 14. 【-1,1】 15.(-1,1) 16.
14. 【-1,1】 15.(-1,1) 16. 17.
17.
18、解: (1)由函数 的图像与x轴的任意两个相邻交点间的距离为
的图像与x轴的任意两个相邻交点间的距离为 得函数周期为
得函数周期为 ,
,

 直线
直线 是函数
是函数 图像的一条对称轴,
图像的一条对称轴, ,
,
 或
或 ,
, ,
,
 ,
,
 .
.  .
.
(2)

 ,
,
即函数 的单调递增区间为
的单调递增区间为 . ,
. ,
19、解:(1)设公比为q,由题知:2( )=
)= +
+
∴ ,即
,即
∴q=2,即
(2) ,所以
,所以 ①
①
 ②
②
①-②:
∴
 20、解:(Ⅰ) 由题知:
20、解:(Ⅰ) 由题知: ,
,
又∵平面 平面
平面 且交线为
且交线为
∴ 
∴
又∵ ,且
,且
∴ 
(Ⅱ)在平面ABCE内作 .
.
∵平面 平面
平面 且交线为
且交线为
∴  ∴
∴  就是
就是 与平面
与平面 所成角
所成角
由题易求CF=1,DF=5,则
21、解:(1)f(x)=ax3 4ax2+4ax
4ax2+4ax
f/(x)=3ax2 8ax+
8ax+ 2)(x
2)(x 2)=0
2)=0 x=
x= 或2
或2
∵f(x)有极大值32,而f(2)=0 ∴f( )=
)= ,a=1
,a=1
(2)f/(x)=a(3x 2)(x
2)(x 2)
2)
当a>0时,f(x)=[  2,
2, ]上递增在[
]上递增在[ ]上递减,
]上递减, ,
,
∴0<a<27
当a<0时,f(x)在[ 2,
2, ]上递减,在[
]上递减,在[ ]上递增,f(
]上递增,f( 2)=
2)=

 ,即
,即
∴  综上
综上 
22、解(1)设过抛物线 的焦点
的焦点 的直线方程为
的直线方程为 或
或 (斜率
(斜率 不存在),则
不存在),则  得
得 ,
,
当 (斜率
(斜率 不存在)时,则
不存在)时,则
又
 ,
, 所求抛物线方程为
所求抛物线方程为
(2)设
由已知直线 的斜率分别记为:
的斜率分别记为: ,得
,得




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com