练习册

  • 练习册
  • 试题
    △ABC的外接圆半径为1.角A.B.C的对边分别为a.b.c.向量满足m∥n. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分10分）选修4—1：几何证明选讲   如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D。

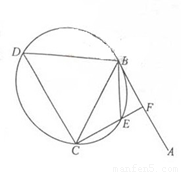
    （Ⅰ）证明：DB=DC；

    （Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径。

     

    查看答案和解析>>

    （本小题满分10分）选修4—1：几何证明选讲  如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于D。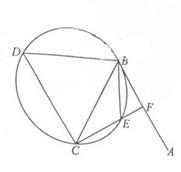

    （Ⅰ）证明：DB=DC；
    （Ⅱ）设圆的半径为1，BC=，延长CE交AB于点F，求△BCF外接圆的半径。

    查看答案和解析>>

    1―5  BCCCD    6―10  ACBBA     11―12   AC

    13.  3    14.  高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。    15.  2    16.  高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    17.解：（1）因为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    因为三角形ABC的外接圆半径为1，由正弦定理，得高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    于是高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    因为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。故三角形ABC是直角三角形  

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。因为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，故高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （2）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    设高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。则高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。因为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。故高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上单调递减函数.

    所以高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。所以实数的取值范围是高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    18.解：（1）3名志愿者恰好连续3天参加社区服务工作的概率为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

          （2）随机变量高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的分布列为：

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    0

    1

    2

    3

    P

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    19.解：（1）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。正方形ABCD，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    又二面角高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是直二面角

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    又高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。ABEF是矩形，G是EF的中点，

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。   高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。又高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    而高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。故平面高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （2）由（1）知平面高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。且交于GC，在平面BGC内作高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。垂足为H，则高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是BG与平面AGC所成的角.

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。.

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。即BG与平面AGC所成的角为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （3）由（2）知高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。作高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。垂足为O，连接HO，则高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为二面角高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的平面角

    在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。ABG中, 高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中, 高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。中, 高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    20.解：（1）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    ①当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。故高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为减，

    在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为增，在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为减.

    ②当高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。故高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为减，

    在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为增，在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上为减.

    （2）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的取值范围是高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    21.解：设高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。与高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。联立的高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

            高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （Ⅰ）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

                  高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

         高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （Ⅱ）（1）过点A的切线：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    过点B的切线：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    联立得点高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    所以点N在定直线高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。上

    （2）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    联立：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    可得  高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    直线MN：高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。轴的截距为高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。直线MN在高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。轴上截距的取值范围是高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    22.解：（Ⅰ）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （1）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时，高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时不等式成立

    （2）假设高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时不等式成立，即高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。时不等式成立

    由（1）（2）可知，对高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。都有高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    （Ⅱ）（1）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

                 高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。是递减数列

    （2）高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

    高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。

     

     


    同步练习册答案