（12分）椭圆C：的两个焦点分别为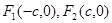 ,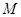是椭圆上一点，且满足。

（1）求离心率e的取值范围；

（2）当离心率e取得最小值时，点N( 0 , 3 )到椭圆上的点的最远距离为。

(i)求此时椭圆C的方程；

(ii)设斜率为的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点P（0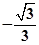，）、Q的直线对称？若能，求出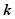的取值范围；若不能，请说明理由。

椭圆G：的两个焦点为F₁、F₂，短轴两端点B₁、B₂，已知F₁、F₂、B₁、B₂四点共圆 ，且点N（0，3）到椭圆上的点的最远距离为

（1）求此时椭圆G的方程；

（2）设斜率为k（k≠0）的直线m与椭圆G相交于不同的两点E、F，Q为EF的中点，问E、F两点能否关于过点的直线对称？若能，求出k的取值范围；若不能，请说明理由。

设，椭圆方程为，抛物线方程为。如图所示，过点

作轴的平行线，与抛物线在第一象限的交点为G。已知抛物线在点

G的切线经过椭圆的右焦点F1。

（1）求满足条件的椭圆方程和抛物线方程；     (6分)

（2）设A、B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得

△ABP为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具

体求出这些点的坐标）。(8分)

设，椭圆方程为，抛物线方程为。如图所示，过点

作轴的平行线，与抛物线在第一象限的交点为G。已知抛物线在点

G的切线经过椭圆的右焦点F1。

（1）求满足条件的椭圆方程和抛物线方程；     (6分)

（2）设A、B分别是椭圆长轴的左、右端点，试探究在抛物线上是否存在点P，使得

△ABP为直角三角形？若存在，请指出共有几个这样的点？并说明理由（不必具

体求出这些点的坐标）。(8分)

（12分）椭圆C：的两个焦点分别为 ,是椭圆上一点，且满足。

（1）求离心率e的取值范围；

（2）当离心率e取得最小值时，点N( 0 , 3 )到椭圆上的点的最远距离为。

(i)求此时椭圆C的方程；

(ii)设斜率为的直线l与椭圆C相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点P（0，）、Q的直线对称？若能，求出的取值范围；若不能，请说明理由。